There are a large number of cells available, each marked (6 V, 0.5 Ω ) to be used to supply current to a device of resistance 0.75Ω requiring 24 A current . How should the cells be arranged , so that maximum power is transmitted to the load using minimum number of cells ?
A. Six rows , each containig four cells
B. Four rows, each containing six cells
C. Four rows, each containing four cells
D. Six rows , each contining six cells .
The correct Answer is:B
To solve the problem of arranging the cells to supply current to a device with a resistance of 0.75Ω while requiring 24A of current, we need to consider the specifications of the cells and the principles of maximum power transfer.
1. Identify the Parameters:
- Each cell has an EMF of 6V and an internal resistance of 0.5Ω.
- The load resistance RL=0.75Ω.
- The required current I=24A.
2. Calculate the Total Voltage Required:
- According to Ohm's Law, the voltage across the load can be calculated as:
VL=I×RL=24A×0.75Ω=18V
3. Determine the Number of Cells Needed in Series:
- The total EMF from n cells in series is:
Vtotal=n×6V
- To find n, set Vtotal equal to VL:
n×6=18⟹n=186=3
4. Calculate the Total Internal Resistance:
- The total internal resistance Rinternal of n cells in series is:
Rinternal=n×0.5Ω=3×0.5=1.5Ω
5. Determine the Total Resistance for Maximum Power Transfer:
- For maximum power transfer, the total resistance Rtotal should equal the load resistance RL:
Rtotal=Rinternal+RL
- Rearranging gives:
Rinternal=RL⟹1.5Ω=0.75Ω
- This indicates that we need to arrange cells in parallel to reduce the internal resistance.
6. Calculate the Number of Parallel Rows:
- Let m be the number of parallel rows. The total internal resistance of m rows of n cells in series is given by:
Rtotal=Rinternalm=1.5m
- Setting this equal to RL:
1.5m=0.75⟹m=1.50.75=2
7. Final Arrangement:
- We need n=3 cells in series and m=2 rows in parallel.
- Therefore, the total number of cells used is:
Total cells=n×m=3×2=6
Conclusion:
To achieve maximum power transfer to the load while using the minimum number of cells, arrange the cells in 2 parallel rows of 3 cells each.
- Each cell has an EMF of 6V and an internal resistance of 0.5Ω.
- The load resistance RL=0.75Ω.
- The required current I=24A.
- According to Ohm's Law, the voltage across the load can be calculated as:
VL=I×RL=24A×0.75Ω=18V
- The total EMF from n cells in series is:
Vtotal=n×6V
- To find n, set Vtotal equal to VL:
n×6=18⟹n=186=3
- The total internal resistance Rinternal of n cells in series is:
Rinternal=n×0.5Ω=3×0.5=1.5Ω
- For maximum power transfer, the total resistance Rtotal should equal the load resistance RL:
Rtotal=Rinternal+RL
- Rearranging gives:
Rinternal=RL⟹1.5Ω=0.75Ω
- This indicates that we need to arrange cells in parallel to reduce the internal resistance.
- Let m be the number of parallel rows. The total internal resistance of m rows of n cells in series is given by:
Rtotal=Rinternalm=1.5m
- Setting this equal to RL:
1.5m=0.75⟹m=1.50.75=2
- We need n=3 cells in series and m=2 rows in parallel.
- Therefore, the total number of cells used is:
Total cells=n×m=3×2=6
To achieve maximum power transfer to the load while using the minimum number of cells, arrange the cells in 2 parallel rows of 3 cells each.
Similar Questions
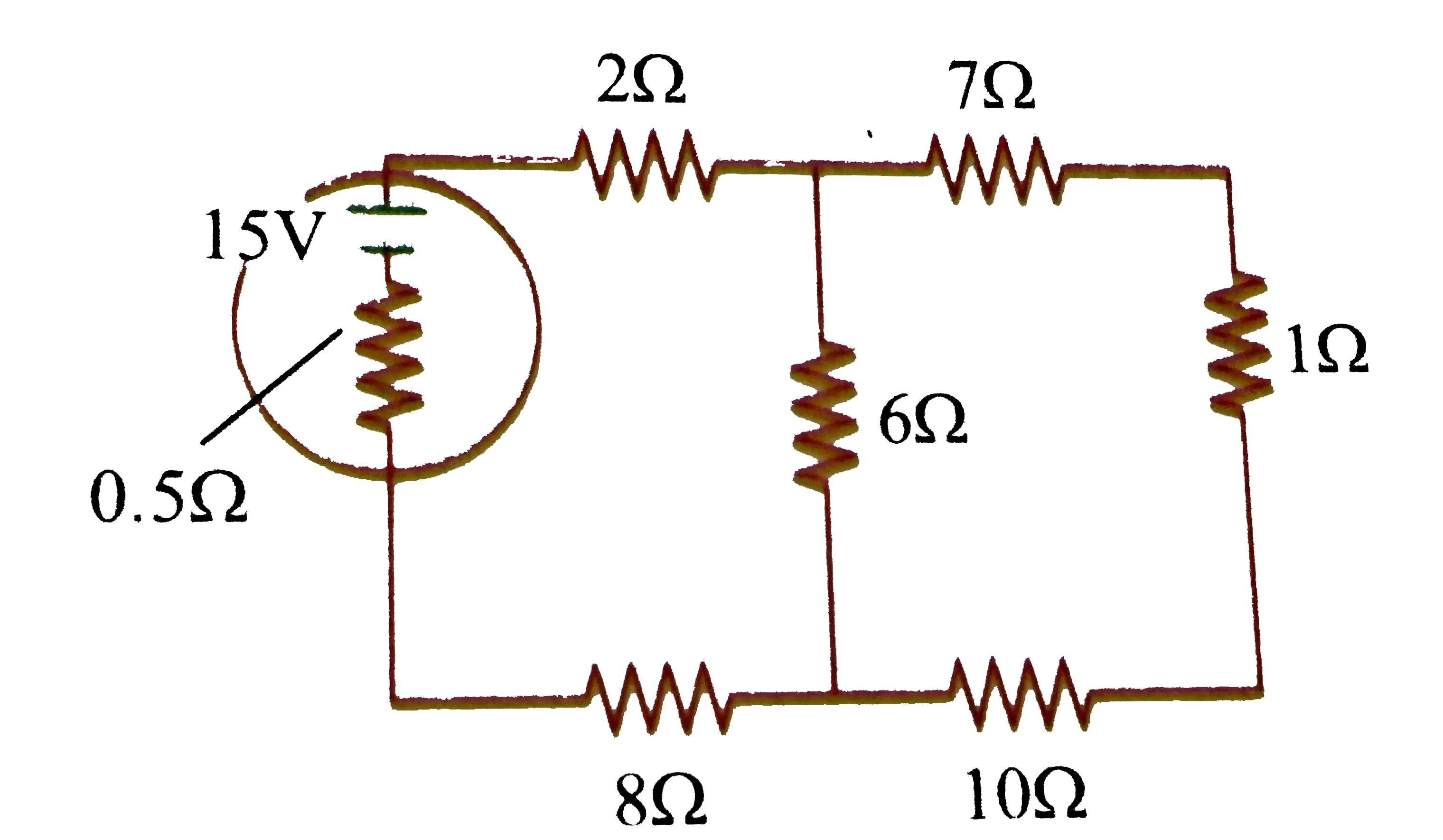
The emf of a cell E is 15 V as shown in the figure with an internal resistance of 0.5Ω. Then the value of the current drawn from the cell is
View SolutionTo get maximum current through a resistance of 2.5Ω, one can use m rows of cells, each row having n cells. The internal resistance of each cell is 0.5Ω what are the values of n and m, if the total number of cells is 45.
View Solution36 cells each of internal resistance 0.5Ω and emf 1.5 V each are used to send current through an external circuit of 2Ω resistance. Find the best mode of grouping them and the current through the external circuit.
View SolutionA cell supplies a current of 2 A when it is connected to a 5Ω resistance and supplies a current of 1.2 A, if it is connected to a resistance of 9 Ω. Find the e.m.f and internal resistance of the cell.
View SolutionSiix lead-acid type of secondary cells, each of emf 2.0 V and internal resistancce 0.015Ω are joined in series to provide a supply to a resistance of 8.5Ω. Determine : (i) the current draw from the fupply and (ii) its terminal voltage.
View SolutionMaximum current produced by a cell of emf 10 V and internal resistance 2Ω is
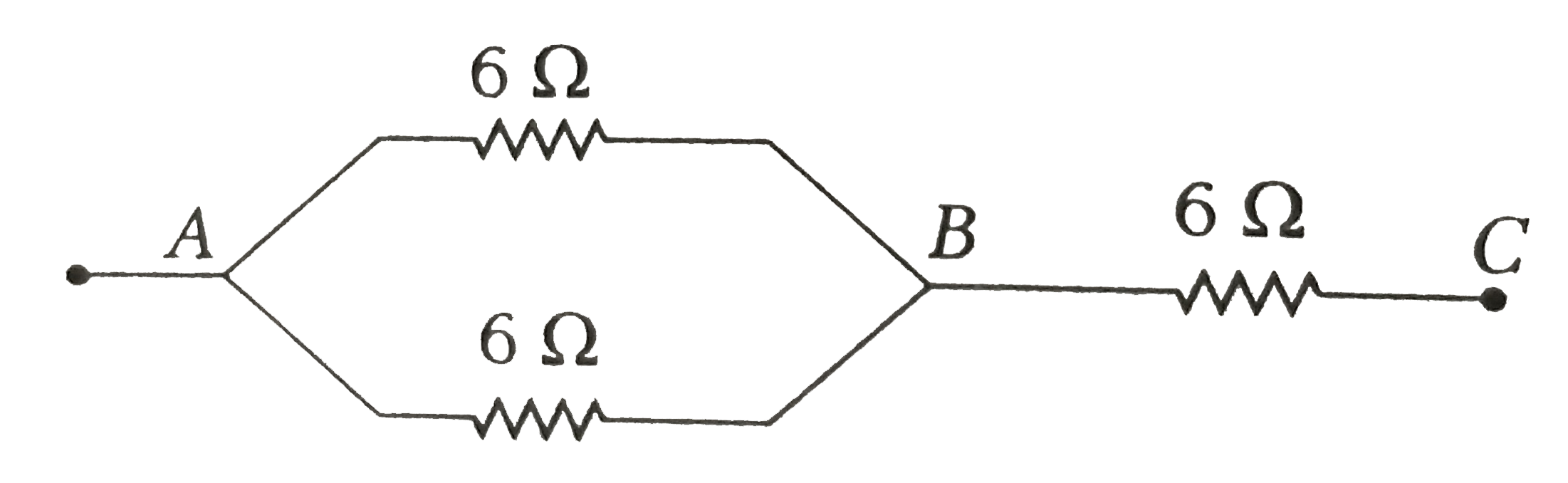
View SolutionIn the following figures, each of the three resistances, the rating of 24 W and resistance of 6Ω. Find the maximum power rating of the circuit.
View SolutionDertermine the current through the battery of internal resistance 0.5Ω for the circuit shown in fig. 7.14. How much power is dissipated in 6ω resistance ?

View SolutionCalculate the current flowing through a wire of resistance 7.5 Ω connected to a battery of potential difference 1.5. V.
View SolutionA galvenometer has a resistance of 50Ω and its full-scale deflection current is 50μA. What resistance should be added to it so that it can have a range of 0−5V?
View Solution
