36 cells each of internal resistance 0.5Ω and emf 1.5 V each are used to send current through an external circuit of 2Ω resistance. Find the best mode of grouping them and the current through the external circuit.
To solve the problem, we need to determine the best mode of grouping the 36 cells and calculate the current flowing through the external circuit. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the given values
- Number of cells (total) = 36
- Internal resistance of each cell (r) = 0.5 Ω
- EMF of each cell (E) = 1.5 V
- External resistance (R) = 2 Ω
Step 2: Determine the configuration of cells
We can arrange the cells in series and parallel combinations. Let’s denote:
- M = number of rows (in series)
- N = number of cells in each row (in parallel)
The total number of cells can be expressed as:
N×M=36
Step 3: Calculate the total resistance in terms of M and N
The total internal resistance (R_internal) for M rows in series is:
Rinternal=M×r=M×0.5
The total resistance of N cells in parallel is given by:
Rparallel=rN=0.5N
The total resistance in the circuit (R_total) is the sum of the external resistance and the internal resistance:
Rtotal=R+Rinternal=2+M×0.5
Step 4: Set up the equation for the external circuit
Using the relationship between the total resistance and the external resistance, we can set up the equation:
0.5N=2+M×0.5
Step 5: Relate N and M
From the equation N×M=36, we can express N in terms of M:
N=36M
Substituting this into the resistance equation gives:
0.536M=2+M×0.5
0.5M36=2+0.5M
Step 6: Solve for M
Multiplying through by 36 to eliminate the fraction:
0.5M=72+18M
Rearranging gives:
0.5M−18M=72
−17.5M=72
M=7217.5≈4.11
Since M must be an integer, we can try M = 3 and M = 4 to find a suitable configuration.
Step 7: Check integer values for M
1. For M = 3:
N=363=12
Rinternal=3×0.5=1.5
Rtotal=2+1.5=3.5
2. For M = 4:
N=364=9
Rinternal=4×0.5=2
Rtotal=2+2=4
Step 8: Calculate the current
Using Ohm's Law:
I=EtotalRtotal
Where Etotal=M×E=M×1.5
For M = 3:
Etotal=3×1.5=4.5
I=4.53.5≈1.29A
For M = 4:
Etotal=4×1.5=6
I=64=1.5A
Final Result
The best mode of grouping the cells is with M = 4 and N = 9, yielding a current of approximately 1.5 A through the external circuit.
- Number of cells (total) = 36
- Internal resistance of each cell (r) = 0.5 Ω
- EMF of each cell (E) = 1.5 V
- External resistance (R) = 2 Ω
We can arrange the cells in series and parallel combinations. Let’s denote:
- M = number of rows (in series)
- N = number of cells in each row (in parallel)
N×M=36
The total internal resistance (R_internal) for M rows in series is:
Rinternal=M×r=M×0.5
Rparallel=rN=0.5N
Rtotal=R+Rinternal=2+M×0.5
Using the relationship between the total resistance and the external resistance, we can set up the equation:
0.5N=2+M×0.5
From the equation N×M=36, we can express N in terms of M:
N=36M
0.536M=2+M×0.5
0.5M36=2+0.5M
Multiplying through by 36 to eliminate the fraction:
0.5M=72+18M
Rearranging gives:
0.5M−18M=72
−17.5M=72
M=7217.5≈4.11
1. For M = 3:
N=363=12
Rinternal=3×0.5=1.5
Rtotal=2+1.5=3.5
N=364=9
Rinternal=4×0.5=2
Rtotal=2+2=4
Using Ohm's Law:
I=EtotalRtotal
Where Etotal=M×E=M×1.5
Etotal=3×1.5=4.5
I=4.53.5≈1.29A
Etotal=4×1.5=6
I=64=1.5A
The best mode of grouping the cells is with M = 4 and N = 9, yielding a current of approximately 1.5 A through the external circuit.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Taking it together
142 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Level 2 Subjective
13 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
The internal resistance of a 2.1V cell which gives a current 0.2A through a resistance of 10Ω
View SolutionThree identical cells, each of emf 2 V and internal resistance 0.2Ω are connected in series to an external resistor of 7.4Ω. Calculate the current in the circuit.
View Solution24 cells, each of emf 1.5V and internal resistance is 2Ω connected to 12Ω series external resistance. Then,
View Solution100 cells each of emf 5V and internal resistance 1Ω are to be arranged to produce maximum current in a 25Ω resistance. Each row contains equal number of cells. Find the number of rows.
View SolutionThe internal resistance of a 2.1 V cell which gives a current of 0.2A through a resistance of 10Ω is
View SolutionIn the given circuit current flowing through 2 Omega resistance is
View SolutionTwo cells having emf's of 10 V and 8 V, and internal resistance of 1Ω(each) are connected as shown with an external resistance of 8Ω Find the current flowing through the circuit.
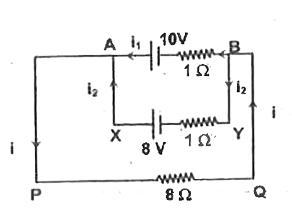
View SolutionA cell of internal resistance r drivers current through an external resistance R. The power delivered by the to the external resistance will be maximum when:
View SolutionIn the circuit in figure, the current flowing 5Ω resistance is :
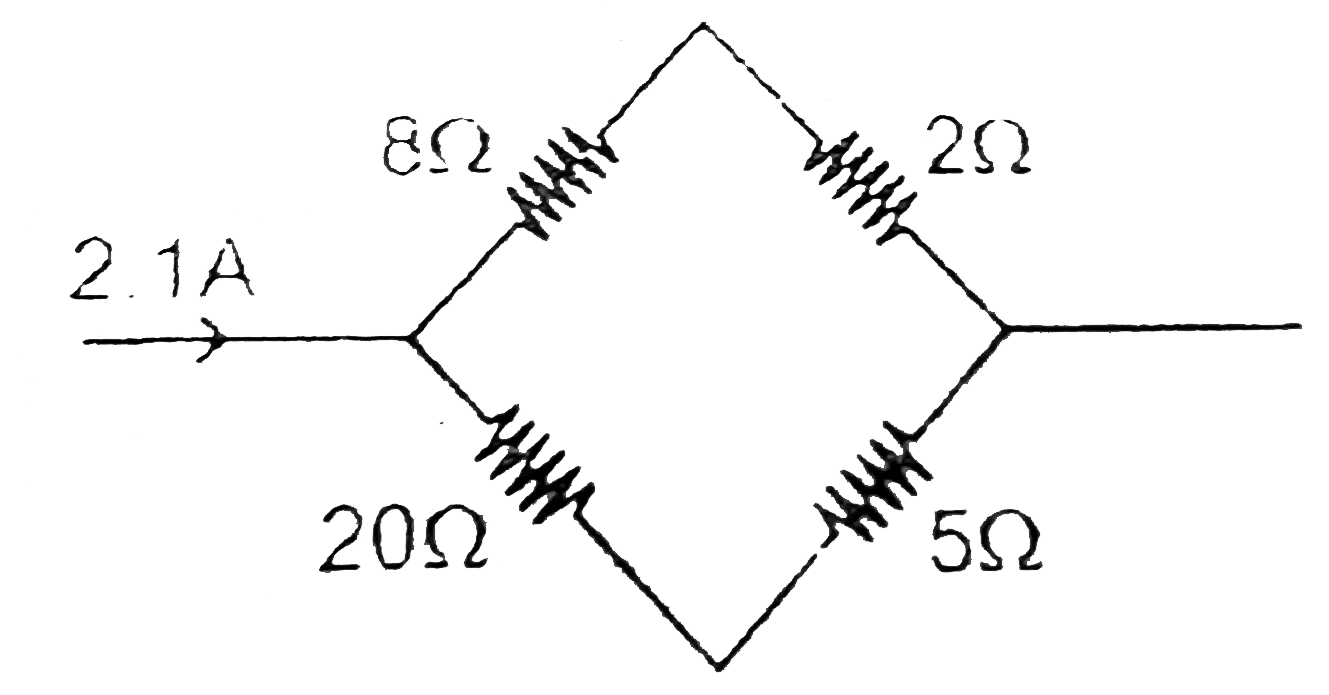
View SolutionIn the circuit of adjoining figure the current through 12Ω resister will be
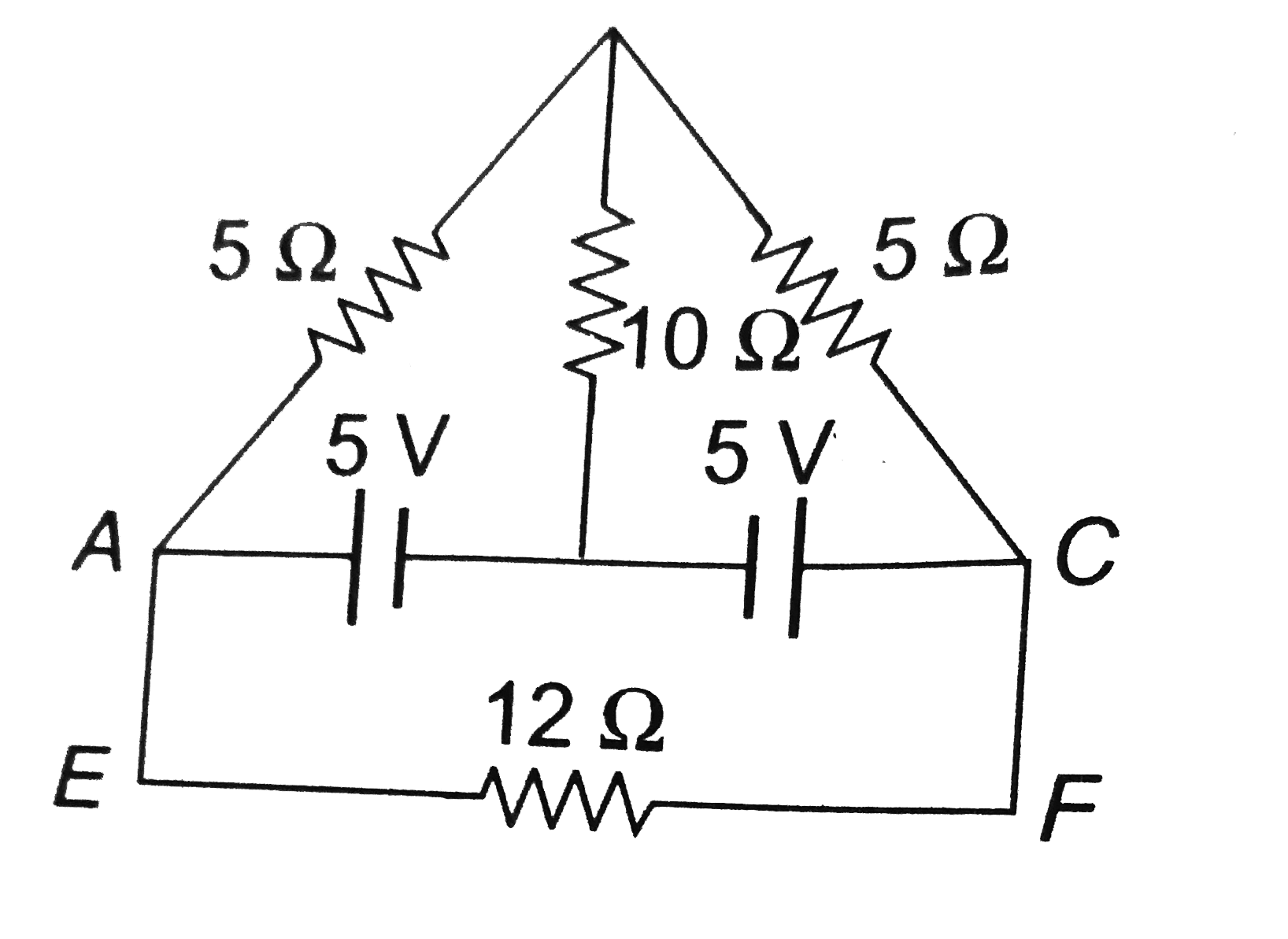
View Solution
