A galvanometer having a resistance of 8 ohm is shunted by a wire of resistance 2 ohm . If the total current is 1 amp , the part of it passing through the shunt will be
0.2A
0.8A
0.25A
0.5A
The correct Answer is:B
To solve the problem step by step, we will use the principles of parallel circuits and Ohm's law.
Step 1: Identify the given values
- Resistance of the galvanometer (G) = 8 ohms
- Resistance of the shunt (Rs) = 2 ohms
- Total current (I) = 1 ampere
Step 2: Calculate the equivalent resistance (R) of the parallel circuit
The formula for the equivalent resistance of two resistors in parallel is given by:
1R=1G+1Rs
Substituting the values:
1R=18+12
To calculate this, we find a common denominator:
1R=18+48=58
Now, taking the reciprocal to find R:
R=85=1.6 ohms
Step 3: Calculate the total voltage (V) in the circuit
Using Ohm's law, V=I×R:
V=1 A×1.6 ohms=1.6 volts
Step 4: Calculate the current through the shunt (I2)
Since the galvanometer and the shunt are in parallel, the voltage across them is the same. We can use Ohm's law again:
V=I2×Rs
Rearranging gives:
I2=VRs
Substituting the known values:
I2=1.6 volts2 ohms=0.8 amperes
Final Answer
The part of the total current passing through the shunt is 0.8 amperes.
---
- Resistance of the galvanometer (G) = 8 ohms
- Resistance of the shunt (Rs) = 2 ohms
- Total current (I) = 1 ampere
The formula for the equivalent resistance of two resistors in parallel is given by:
1R=1G+1Rs
Substituting the values:
1R=18+12
To calculate this, we find a common denominator:
1R=18+48=58
Now, taking the reciprocal to find R:
R=85=1.6 ohms
Using Ohm's law, V=I×R:
V=1 A×1.6 ohms=1.6 volts
Since the galvanometer and the shunt are in parallel, the voltage across them is the same. We can use Ohm's law again:
V=I2×Rs
Rearranging gives:
I2=VRs
Substituting the known values:
I2=1.6 volts2 ohms=0.8 amperes
The part of the total current passing through the shunt is 0.8 amperes.
Similar Questions
A galvanometer of resistance G is shunted by a resistance Sohm. To keep the main current in the circuit uncharged, the resistnace to be put in series with the galvonmeter
View SolutionA galvanometer of resistance 20Ω is shunted by a 2Ω resistor. What part of the main current flows through the galvanometer ?
View SolutionA galvanometer has a resistance of 3663Ω. A shunt S is connected across it such that (1/34) of the total current passes through the galvanometer. Then the value of the shunt is
View SolutionA galvanometer has a resistance of 3663Ω. A shunt S is connected across it such that (1/34) of the total current passes through the galvanometer. Then the value of the shunt is
View SolutionA galvanometer of resistance 150 ohm is shunted such that only 1/11 of the main current flows through the galvanometer. The resistance of the shunt is, (in ohm)
View SolutionWe have a galvanometer of resistance 25Ω. It is shunted by a 2.5Ω wire. The part of total current that flows through the galvanometer is given as
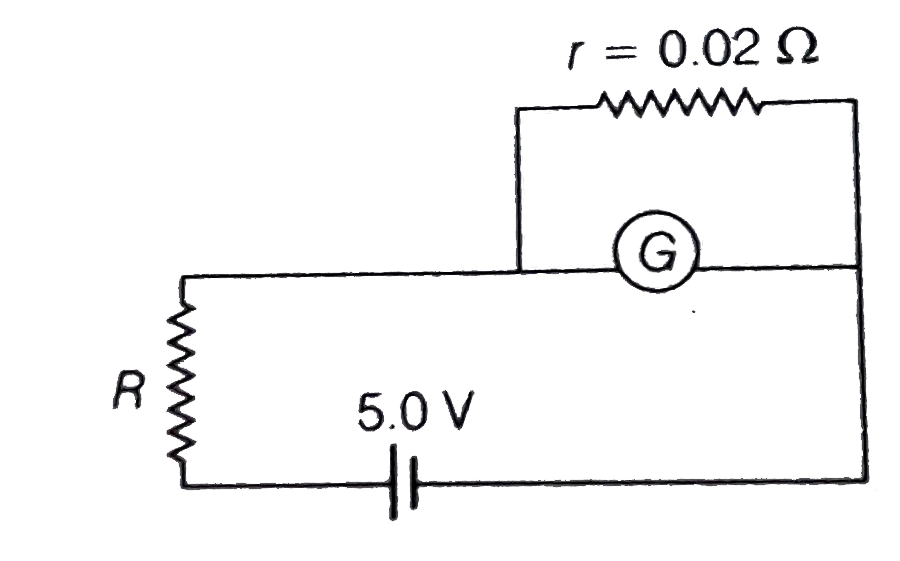
View SolutionIn the circuit, shown the galvanometer G of resistance 60Ω is shifted by a resistance r=0.02Ω. The current through R is nearly 1A. The value of resistance R (in ohm) is nearly.
View SolutionA galvanometer has resistance 500 ohm. It is shunted so that its sensitivity decreases by 100 times. Find the shunt resistance.
View SolutionA galvanometer has a resistance of 98Ω. If 2% of the main current is to be passed through the meter what should be the value of the shunt?
View SolutionA current of 2 A is passed through a coil of resistance 75 ohm for 2 minutes
How much charge is passed through the resistance ?
View Solution
