A galvanometer has resistance 500 ohm. It is shunted so that its sensitivity decreases by 100 times. Find the shunt resistance.
To solve the problem, we need to find the shunt resistance (denoted as Rs) that decreases the sensitivity of a galvanometer by 100 times. Here are the steps to derive the solution:
Step 1: Understand the problem
A galvanometer has a resistance Rg=500Ω. When a shunt resistance Rs is added in parallel, the sensitivity of the galvanometer decreases by a factor of 100. This means the new equivalent resistance Req is given by:
Req=Rg⋅RsRg+Rs
And it is equal to Rg100.
Step 2: Set up the equation
From the problem, we can express the equivalent resistance as:
Req=500⋅Rs500+Rs
According to the problem, this equivalent resistance is:
Req=500100=5Ω
So we can set up the equation:
500⋅Rs500+Rs=5
Step 3: Cross-multiply to eliminate the fraction
Cross-multiplying gives:
500⋅Rs=5(500+Rs)
Step 4: Expand and rearrange the equation
Expanding the right side:
500⋅Rs=2500+5Rs
Now, rearranging the equation to isolate Rs:
500Rs−5Rs=2500
495Rs=2500
Step 5: Solve for Rs
Now, divide both sides by 495:
Rs=2500495
Calculating this gives:
Rs≈5.05Ω
Final Answer
Thus, the shunt resistance Rs is approximately 5.05Ω.
---
A galvanometer has a resistance Rg=500Ω. When a shunt resistance Rs is added in parallel, the sensitivity of the galvanometer decreases by a factor of 100. This means the new equivalent resistance Req is given by:
Req=Rg⋅RsRg+Rs
And it is equal to Rg100.
From the problem, we can express the equivalent resistance as:
Req=500⋅Rs500+Rs
According to the problem, this equivalent resistance is:
Req=500100=5Ω
So we can set up the equation:
500⋅Rs500+Rs=5
Cross-multiplying gives:
500⋅Rs=5(500+Rs)
Expanding the right side:
500⋅Rs=2500+5Rs
Now, rearranging the equation to isolate Rs:
500Rs−5Rs=2500
495Rs=2500
Now, divide both sides by 495:
Rs=2500495
Calculating this gives:
Rs≈5.05Ω
Thus, the shunt resistance Rs is approximately 5.05Ω.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA
142 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
In an attempt to increases the current sensitivity of a moving coil galvanometer, it is found that its resistance becomes double while the current sensitivity increases by 10%. The voltage sensitivity of the galvanometer changes by
View SolutionTo increase the current sensitivity of a moving coil galvanometer by 50% its resistance is increased so that the new resistance becomes twice its initial resistance. By what factor does its voltage sensitivity change?
View SolutionA galvanometer of resistance 150 ohm is shunted such that only 1/11 of the main current flows through the galvanometer. The resistance of the shunt is, (in ohm)
View SolutionA galvanometer having a resistance of 8 ohm is shunted by a wire of resistance 2 ohm . If the total current is 1 amp , the part of it passing through the shunt will be
View SolutionA galvanometer having a resistance of 8 ohm is shunted by a wire of resistance 2 ohm . If the total current is 1 amp , the part of it passing through the shunt will be
View SolutionThe sensitivity of a galvanometer is 60 divisions/Amp. When a shunt is used, its sensitivity becomes 10 divisions/amp. If galvanometer is of resistance 20Ω, · the value of shunt used is :
View SolutionIn the given circuit, a galvanometer with a resistance of 70Ω is converted to an ammeter 0.05Ω by a shunt resistance of 0.052, total current measured by this device
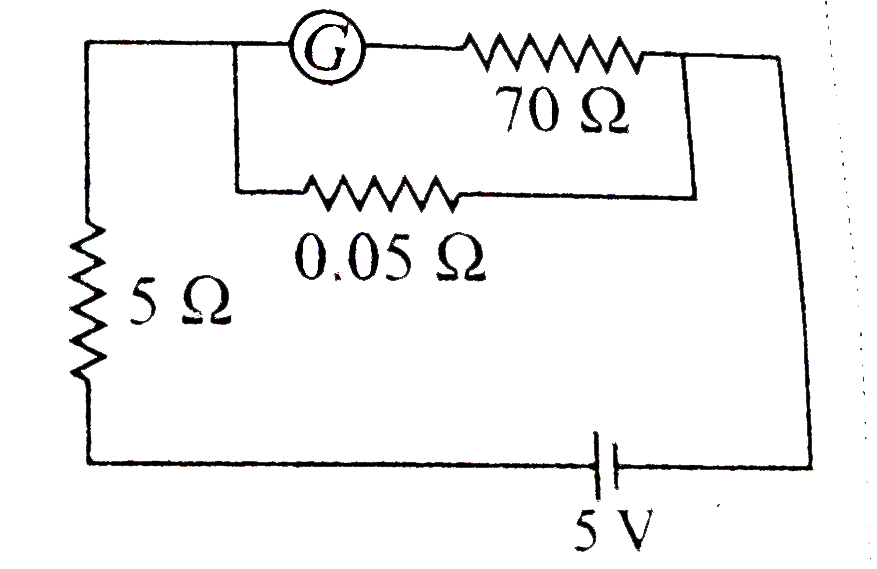
View SolutionA galvanometer measures current which passes through it. A galanometer can measure typically carrent of order of mA. To be able to measure currents of the order of amperes of main current, a shunt resistance 'S' is connected in parallel with galvanometer.
If resistance of galavonometer is 10Ω and maximum current ig is 10mA then the shunt resistance required so that the main current 'I' can be upto 1A is (in Ω)
View SolutionIn a meter bride, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10cm . Find the unknown resistance X.
View SolutionIn a meter bridge, null point is 20cm, when the known resistance R is shunted by 10Ω resistance, null point is found to be shifted by 10 cm. Find the unknown resistance X.
View Solution
