A : A low voltage supply from which high currents are to be withdraw , must have very low internal resistance .
R : Maximum current drawn from a source is inversely proprtional to internal reisistance .
If both Assertion & Reason are true and the reason is the correct explanation of the assertion , then mark
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion then mark.
If Assertion is ture statement but Reason is false , then mark
If both Assertion and Reason are false statements then mark.
The correct Answer is:A
To solve the question, we need to analyze the assertion (A) and the reason (R) provided.
Step 1: Understand the Assertion (A)
The assertion states that "A low voltage supply from which high currents are to be withdrawn must have very low internal resistance."
- Explanation: For a low voltage supply, if we want to draw a high current, the internal resistance must be low. This is because high current can only be achieved if the resistance does not limit the flow of current significantly.
Step 2: Understand the Reason (R)
The reason states that "Maximum current drawn from a source is inversely proportional to internal resistance."
- Explanation: According to Ohm's Law, V=I×R, we can rearrange this to find the current I:
I=VR
From this equation, we can see that if the voltage V is constant, the current I is inversely proportional to the resistance R. This means that as the resistance decreases, the current increases, which supports the assertion.
Step 3: Verify Both Statements
Now we need to determine if both the assertion and the reason are true and if the reason correctly explains the assertion.
- Assertion (A): True. A low voltage supply indeed requires low internal resistance to allow high currents to flow.
- Reason (R): True. The reason correctly states that maximum current is inversely proportional to internal resistance.
Step 4: Conclusion
Since both the assertion and the reason are true, and the reason provides a correct explanation for the assertion, we conclude that:
Final Answer: Both assertion and reason are true, and the reason is the correct explanation of the assertion.
The assertion states that "A low voltage supply from which high currents are to be withdrawn must have very low internal resistance."
The reason states that "Maximum current drawn from a source is inversely proportional to internal resistance."
I=VR
From this equation, we can see that if the voltage V is constant, the current I is inversely proportional to the resistance R. This means that as the resistance decreases, the current increases, which supports the assertion.
Now we need to determine if both the assertion and the reason are true and if the reason correctly explains the assertion.
- Reason (R): True. The reason correctly states that maximum current is inversely proportional to internal resistance.
Since both the assertion and the reason are true, and the reason provides a correct explanation for the assertion, we conclude that:
Similar Questions
A : High voltage ( high tension ) supply must have very large internal resistance.
R: If the circuit is accidentally shorted , then the current drawn will not exceed safely limits if internal resistance is high.
View Solution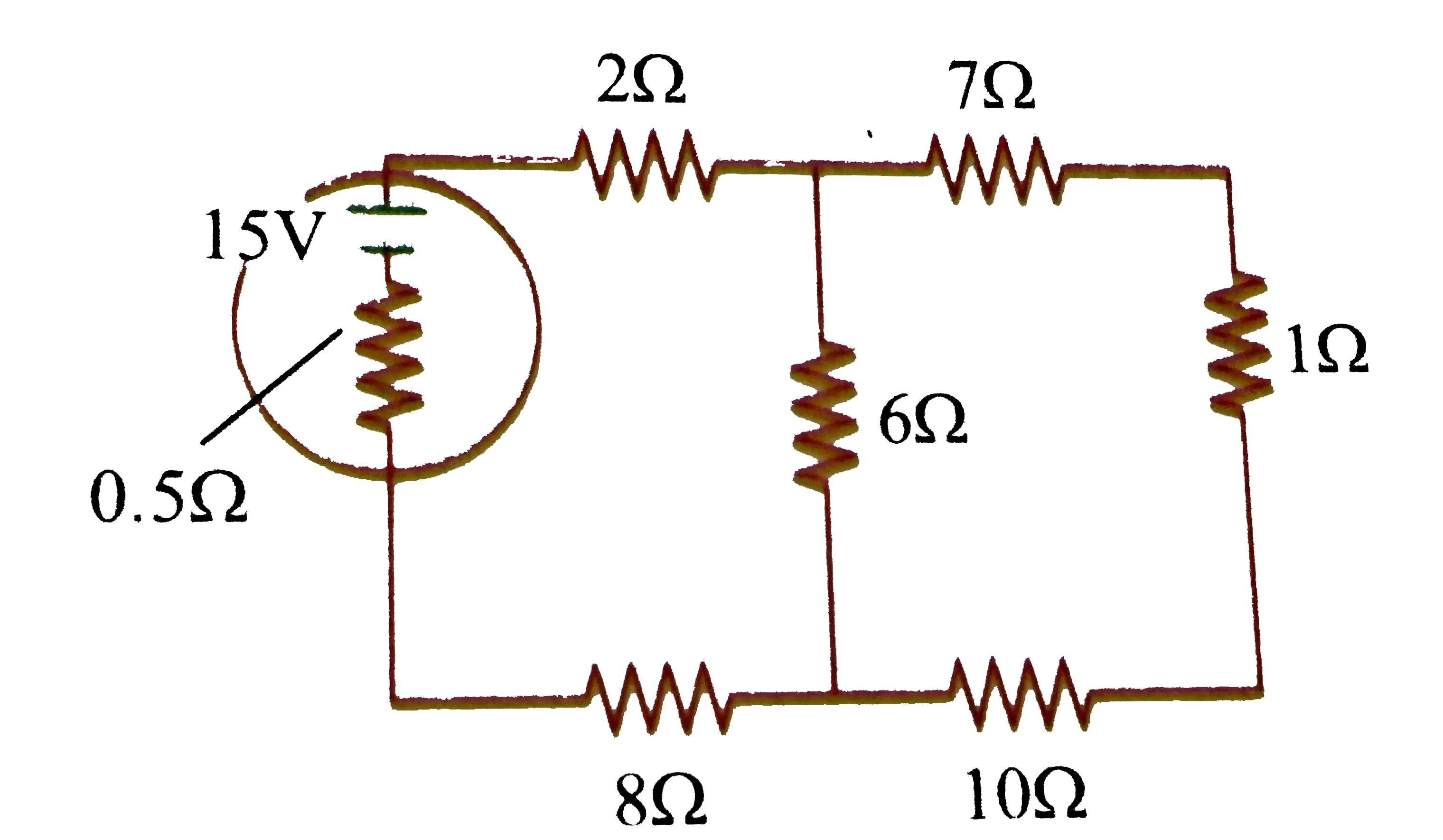
The emf of a cell E is 15 V as shown in the figure with an internal resistance of 0.5Ω. Then the value of the current drawn from the cell is
View Solution
Knowledge Check
In a circuit a cell with internal resistance r is connected to an external resistance R. The condition for the maximum current that drawn from the cell is
AR=rBR<rCR>rDR=0
The maximum current can be drawn from which of the following cells?
View SolutionAn energy source will supply a constant current into the load if its internal resistance is
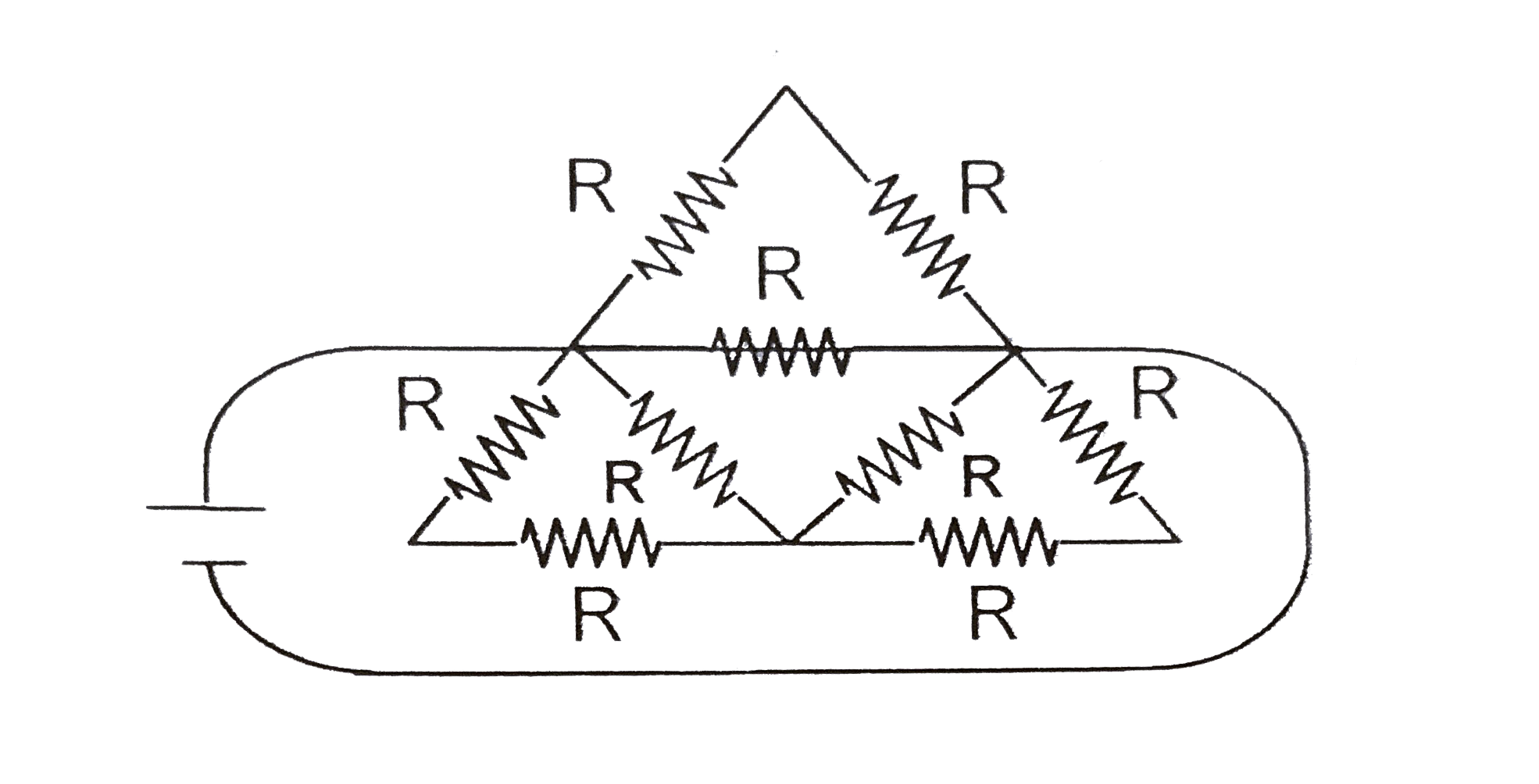
View SolutionFor maximum power from battery the internal resistance of battery r is
View SolutionA car battery of emf 12V and internal resistance 0.05ω receives a current of 60 A from an external source, then the terminal potential difference of the battery is
View Solution24 cells of emf 1.5V each having internal resistance of 1 ohm are connected to an external resistance of 1.5 ohms. To get maximum current,
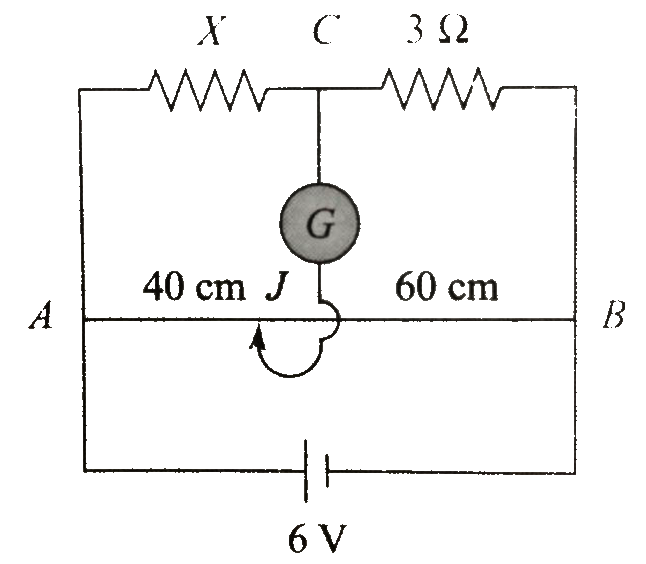
View SolutionIn the gives circuit, a meter bridge is shows in a balanced state. The bridge wire has a resistance of 1Ωcm−1. Find the value of the unknown resistance X and the current draws from the battery of negligible internal resistance.

View SolutionIn the circuit shows in Fig. 6.20, a meter bridge is in its balance state. The meter bridge wire has a resistance of 1Ωcm−1. Calculate the value of the unknow resistance X and current drawn from the battery of negligible internal resistance.
View Solution
