A spring of force constant K is first stretched by distance a from its natural length and then further by distance b. The work done in stretching the part b is
12Ka(a−b)
12Ka(a+b)
12Kb(a−b)
12Kb(2a+b)
The correct Answer is:D
To solve the problem of calculating the work done in stretching a spring by an additional distance b after it has already been stretched by a distance a, we can follow these steps:
Step 1: Understand the work done in stretching a spring
The work done on a spring when it is stretched from its natural length to a distance x is given by the formula:
W=12kx2
where k is the spring constant.
Step 2: Calculate the work done in stretching the spring to distance a+b
When the spring is stretched to a total distance of a+b, the work done is:
Wtotal=12k(a+b)2
Step 3: Calculate the work done in stretching the spring to distance a
The work done in stretching the spring to distance a is:
Wa=12ka2
Step 4: Determine the work done in stretching the spring from a to a+b
The work done in stretching the spring from distance a to a+b (which is the work done in part b) can be calculated by subtracting the work done to stretch to a from the total work done to stretch to a+b:
Wb=Wtotal−Wa
Substituting the expressions we found:
Wb=12k(a+b)2−12ka2
Step 5: Simplify the expression
Now, we simplify Wb:
Wb=12k((a+b)2−a2)
Expanding (a+b)2:
(a+b)2=a2+2ab+b2
Thus, substituting back:
Wb=12k(a2+2ab+b2−a2)
This simplifies to:
Wb=12k(2ab+b2)
Step 6: Factor out the common terms
We can factor out b from the expression:
Wb=12kb(2a+b)
Final Answer
The work done in stretching the part b is:
Wb=12kb(2a+b)
---
The work done on a spring when it is stretched from its natural length to a distance x is given by the formula:
W=12kx2
where k is the spring constant.
When the spring is stretched to a total distance of a+b, the work done is:
Wtotal=12k(a+b)2
The work done in stretching the spring to distance a is:
Wa=12ka2
The work done in stretching the spring from distance a to a+b (which is the work done in part b) can be calculated by subtracting the work done to stretch to a from the total work done to stretch to a+b:
Wb=Wtotal−Wa
Substituting the expressions we found:
Wb=12k(a+b)2−12ka2
Now, we simplify Wb:
Wb=12k((a+b)2−a2)
Expanding (a+b)2:
(a+b)2=a2+2ab+b2
Thus, substituting back:
Wb=12k(a2+2ab+b2−a2)
This simplifies to:
Wb=12k(2ab+b2)
We can factor out b from the expression:
Wb=12kb(2a+b)
The work done in stretching the part b is:
Wb=12kb(2a+b)
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - C)
80 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)
64 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
An elastic string of unstretched length L and force constant k is stretched by a small length x. It is further stretched by another small length y. The work done in second stretching is
View SolutionA spring of force constant K is cut in two parts at its one third length. When both the parts are stretched by same amount, the work done in the two parts, will be :−
View Solution
Knowledge Check
A wire is stretched by one mm by a force of 1 kN. The work done is stretching the wire is
A5 ergsB5 JoulesC0.5 ergsD0.5 Joules
A spring of force constant k is cut in two parts at its one-third lingth. When both the parts are stretched by same amount. The word done in the two parts will be .
View SolutionAn elastic spring of unstretched length L and spring constant K is stretched by a small length x. It is further stretched by another small length y. the work done in second stretcing is
View SolutionA rod of mass M and length L is hinged at its one end and carries a particle of mass m at its lower end. A spring of force constant k1 is installed at distance a from the hinge and another of force constant k2 at B distance b as shown in the figure. If the whcich arrangement rests on a smoth horizontal table top, the frequency of vibration is :
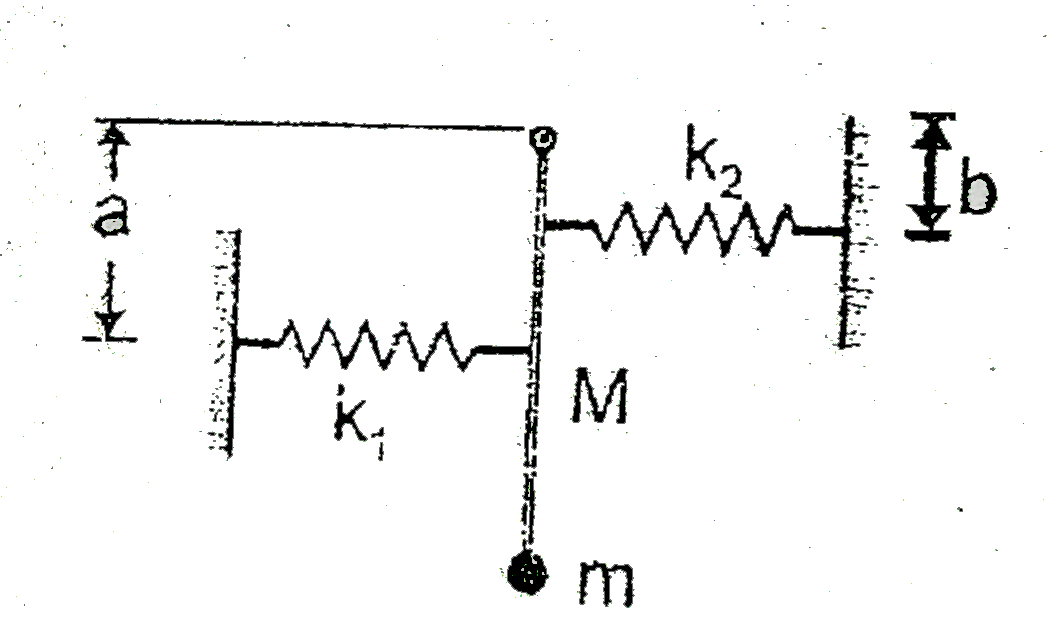
View SolutionA spring, which is initially in its unstretched condition, is first stretched by a length x and then again by a further length x. The work done in the first case is W1 and in the second case is W2.
View SolutionFor the system shown in fig., initially the spring is compressed by a distance 'a' from its natural length and when released, it moves to a distance 'b' from its equillibrium position, the decrease in amplitude for half cycle (-a to +b) is :

View SolutionIf a spring of force constant 'k' is cut into two parts, such that one part is thrice in length of the other part. Then the force constant of each part are
View SolutionA string of length L and force constant k is stretched to obtain extension l. It is further stretched to obtain extension l1. The work done in second stretching is
View Solution
