A particle of mass m attached to the end of string of length l is released from the horizontal position. The particle rotates in a circle about O as shown When it is vertically below O, the string makes contact with a nail N placed directly below O at a distance h and rotates around it. For the particle to swing completely around the nail in a circle.
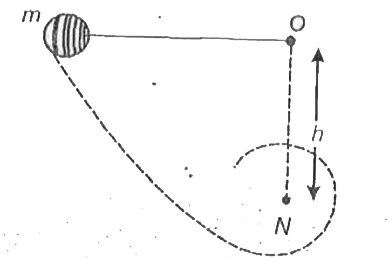
h<35l
h≥35l
h<25l
h≥25l
The correct Answer is:B
Step by step video & image solution for A particle of mass m attached to the end of string of length l is released from the horizontal position. The particle rotates in a circle about O as shown When it is vertically below O, the string makes contact with a nail N placed directly below O at a distance h and rotates around it. For the particle to swing completely around the nail in a circle. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - C)
80 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)
64 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
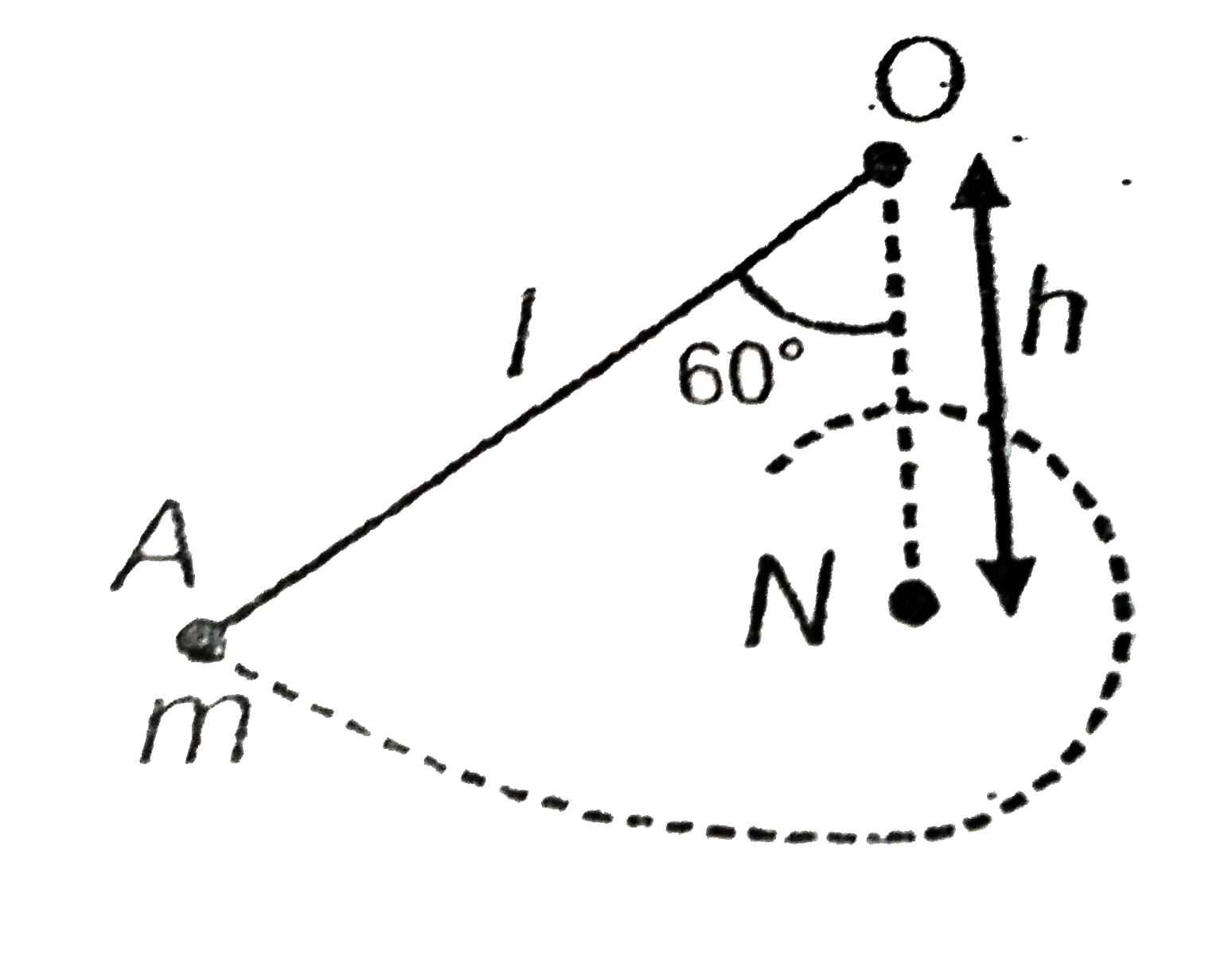
A particle of mass m, attached to the end of string of length l is released from the initial position A as shown in the figures. The particle moves in a vertical circular path about O. When it is vetically below O, the string makes contact with nail N placed directly below O at distance h and rotat es around it. If the particle just complete the vertical circle about N,then
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA particle of mass 'm' is attached to one end of a string of length 'l' while the other end is fixed to a point 'h' above the horizontal table, the particle is made to revolve in a circle on the table, so as to make P revolution per sec. The maximum value of P if the particle is to be contact with the table is
View SolutionA bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
View SolutionTwo particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View SolutionA particle of mass m is fixed to one end of a light rigid rod of length l and rotated in a vertical ciorcular path about its other end. The minimum speed of the particle at its highest point must be
View SolutionA particle of mass m is attached to a string of length L and given velocity √10gL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (i) lowest position (ii) highest position,
View SolutionA mass is attached to the end of a string of length l which is tied to a fixed point O. The mass is released from the initial horizontal position of the string. Below the point O at what minimum distance a peg P should be fixed so that the mass turns about P and can describe a complete circle in the vertical plane?
View Solution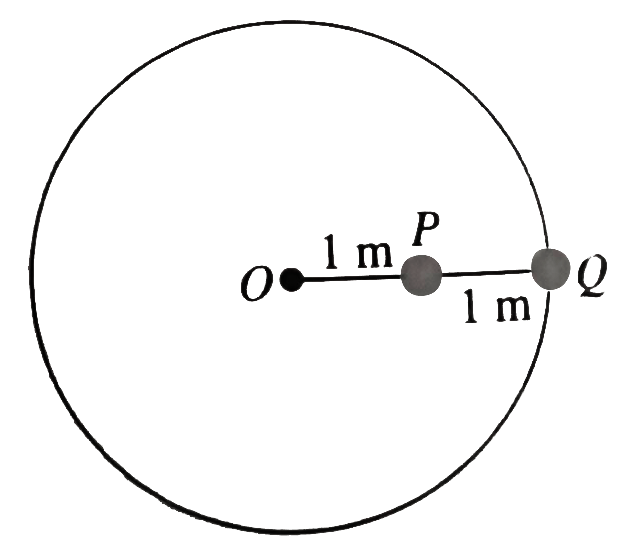
Two spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio:
View Solution
