Two metallic spheres of radii a and b are placed faraway from each other and are connected for a thin conducting wire. A charge Q is given to one of the spheres . Calculate the charge on each sphere at electrostatic equilibrium.
To solve the problem of finding the charge on each metallic sphere at electrostatic equilibrium, we can follow these steps:
Step 1: Understand the System
We have two metallic spheres with radii a and b. Initially, one sphere has a charge Q, and the other is neutral. When connected by a thin conducting wire, charges will redistribute until electrostatic equilibrium is reached.
Step 2: Conservation of Charge
The total charge in the system must remain constant. If we denote the charge on sphere 1 (radius a) as Q1 and the charge on sphere 2 (radius b) as Q2, we can write:
Q1+Q2=Q
Step 3: Equal Potential Condition
At electrostatic equilibrium, both spheres must be at the same electric potential. The potential V of a charged sphere is given by:
V=kQr
where k is Coulomb's constant, Q is the charge on the sphere, and r is the radius of the sphere.
Thus, for the two spheres, we have:
kQ1a=kQ2b
Cancelling k from both sides, we get:
Q1a=Q2b
Step 4: Express Q2 in Terms of Q1
From the equation above, we can express Q2 in terms of Q1:
Q2=baQ1
Step 5: Substitute Q2 into the Charge Conservation Equation
Now, substituting Q2 into the conservation of charge equation:
Q1+baQ1=Q
Factoring out Q1:
Q1(1+ba)=Q
Step 6: Solve for Q1
To isolate Q1:
Q1=Q1+ba=Qa+ba=aQa+b
Step 7: Calculate Q2
Now that we have Q1, we can find Q2:
Q2=baQ1=ba⋅aQa+b=bQa+b
Final Result
Thus, the charges on the spheres at electrostatic equilibrium are:
Q1=aQa+b
Q2=bQa+b
We have two metallic spheres with radii a and b. Initially, one sphere has a charge Q, and the other is neutral. When connected by a thin conducting wire, charges will redistribute until electrostatic equilibrium is reached.
The total charge in the system must remain constant. If we denote the charge on sphere 1 (radius a) as Q1 and the charge on sphere 2 (radius b) as Q2, we can write:
Q1+Q2=Q
At electrostatic equilibrium, both spheres must be at the same electric potential. The potential V of a charged sphere is given by:
V=kQr
where k is Coulomb's constant, Q is the charge on the sphere, and r is the radius of the sphere.
kQ1a=kQ2b
Cancelling k from both sides, we get:
Q1a=Q2b
From the equation above, we can express Q2 in terms of Q1:
Q2=baQ1
Now, substituting Q2 into the conservation of charge equation:
Q1+baQ1=Q
Factoring out Q1:
Q1(1+ba)=Q
To isolate Q1:
Q1=Q1+ba=Qa+ba=aQa+b
Now that we have Q1, we can find Q2:
Q2=baQ1=ba⋅aQa+b=bQa+b
Thus, the charges on the spheres at electrostatic equilibrium are:
Q1=aQa+b
Q2=bQa+b
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:EXERCISE
Explore 20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - A
Explore 44 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:SECTION-J Aakash Challengers Questions
Explore 5 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 15 Videos
Similar Questions
Two metal spheres of same radius R are placed at a very large distance from each other, and they are connected by a coil of inductance L, as it is shown in the figure. One of the spheres is loaded with electric charge. At what time, after closing the switch S. does the charge on this sphere decreases to half ?
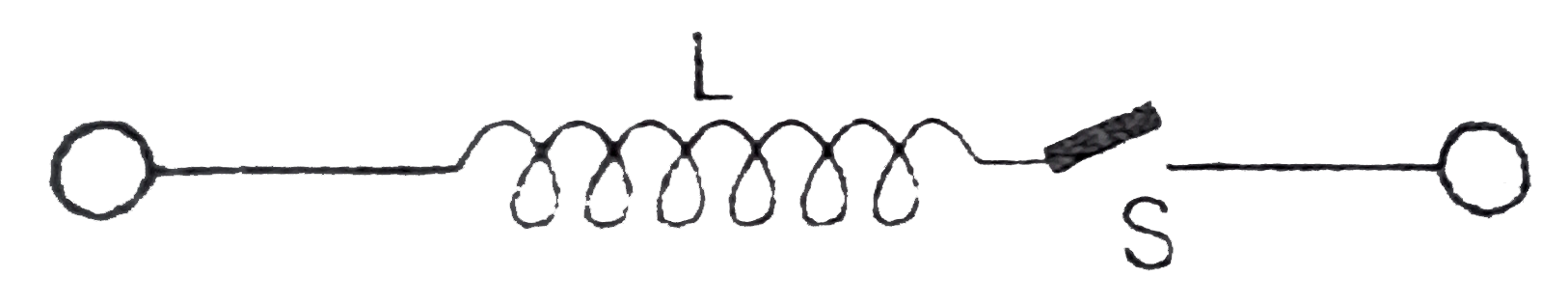
View SolutionConisder a neutral conducting sphere. A poistive point charge is placed outisde the sphere. The net charge on the sphere is then
View SolutionConisder a neutral conducting sphere. A poistive point charge is placed outisde the sphere. The net charge on the sphere is then
View SolutionTwo metallic spheres of radii 1cm and 2cm are given charges 10−2C and 5×10−2C respectively. If they are connected by a conducting wire, the final charge on the smaller sphere is
View SolutionTwo small metal spheres A and B, each of radius r and supported on insulating stands, located at a distance a(a>>r) from each other are connected by a thin conducting wire. A point charge q is brought near the spheres at distance l(l>>r) on the line joining the centers of the spheres. What are the moduli of charge induced on the spheres ?
 .
.
View SolutionTwo metal spheres of radii a and b are connected by a thin wire. Their separation is very large compared to their dimensions. The capacitance of this system is
View SolutionTwo spheres of same metal have radii a and b . They have been connected to a conducting wire. Find the ratio of the electric field intensity upon them.
View SolutionTwo isolated metallic solid spheres of radii R and 2R are charged such that both of these have same charge density σ. The spheres are located far away from each other and connected by a thin conducting wire. Find the new charge density on the bigger sphere.
View SolutionTwo spherical cavities of radii a and b are hollowed out from the interior of a neutral conducting sphere of radius R. At the center of each cavity , a point charge is placed . Call these charges qa and qb.
The electric field inside the cavity of radius a at a distance r from the center of cavity is

View SolutionTwo spherical cavities of radii a and b are hollowed out from the interior of a neutral conducting sphere of radius R. At the center of each cavity , a point charge is placed . Call these charges qa and qb.
The electric field at a distance r outside the conductor is

View Solution
