We know that the gravitational field strength is zero insdie a spereical shell of matter. The electrical field strenght is zero not only insdie an isolated charged spherical conductor but inside an isolated cunductor of any shap . Is the gravitational field strength inside, say, a cubical shell of matter zer? if not, in what respect is the analogy not complete?
To solve the question, we need to analyze the gravitational field strength inside a cubical shell of matter and compare it to the electric field inside a conductor.
1. Understanding Gravitational Field Inside a Spherical Shell:
- It is known that the gravitational field strength inside a spherical shell of uniform mass distribution is zero. This is due to the symmetry of the shell, where the gravitational forces from different parts of the shell cancel each other out at any point inside the shell.
2. Considering a Cubical Shell:
- Now, let’s consider a cubical shell of matter. Unlike a spherical shell, a cubical shell does not have the same symmetry. The mass in a cubical shell does not concentrate at a single point (like the center of a sphere) but is distributed throughout the volume of the cube.
3. Gravitational Field Strength Inside the Cubical Shell:
- Because of the lack of symmetry in a cubical shell, the gravitational field strength inside it is not zero. The gravitational forces from different parts of the cube do not cancel out completely, leading to a net gravitational field inside the cube.
4. Comparison with Electric Field in Conductors:
- In conductors, free electrons move in response to electric fields and redistribute themselves until the electric field inside the conductor is zero. This is true for conductors of any shape, not just spherical ones. The electrons arrange themselves to ensure that the electric field inside the conductor cancels out.
5. Conclusion:
- The analogy between gravitational fields in shells and electric fields in conductors is not complete because the gravitational field inside a cubical shell is not zero due to the lack of symmetry, while the electric field inside a conductor is zero irrespective of its shape due to the behavior of free electrons.
Final Answer:
The gravitational field strength inside a cubical shell of matter is not zero because the mass is not concentrated at a single point and does not have the symmetry required for cancellation of forces. In contrast, the electric field inside any conductor is zero due to the redistribution of free electrons.
- It is known that the gravitational field strength inside a spherical shell of uniform mass distribution is zero. This is due to the symmetry of the shell, where the gravitational forces from different parts of the shell cancel each other out at any point inside the shell.
- Now, let’s consider a cubical shell of matter. Unlike a spherical shell, a cubical shell does not have the same symmetry. The mass in a cubical shell does not concentrate at a single point (like the center of a sphere) but is distributed throughout the volume of the cube.
- Because of the lack of symmetry in a cubical shell, the gravitational field strength inside it is not zero. The gravitational forces from different parts of the cube do not cancel out completely, leading to a net gravitational field inside the cube.
- In conductors, free electrons move in response to electric fields and redistribute themselves until the electric field inside the conductor is zero. This is true for conductors of any shape, not just spherical ones. The electrons arrange themselves to ensure that the electric field inside the conductor cancels out.
- The analogy between gravitational fields in shells and electric fields in conductors is not complete because the gravitational field inside a cubical shell is not zero due to the lack of symmetry, while the electric field inside a conductor is zero irrespective of its shape due to the behavior of free electrons.
The gravitational field strength inside a cubical shell of matter is not zero because the mass is not concentrated at a single point and does not have the symmetry required for cancellation of forces. In contrast, the electric field inside any conductor is zero due to the redistribution of free electrons.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - EXERCISE
20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - A
44 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-J Aakash Challengers Questions
5 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
A : The gravitational field intensity is zero everywhere inside a uniform spherical shell
R: The net force on a point mass inside a uniform spherical shell is zero everywhere .
View SolutionA : Gravitational potential is constant everywhere inside a spherical shell .
R : Gravitational field inside a spherical shell is zero everywhere .
View Solution
Knowledge Check
Assertion: In case of charged spherical shells, E-r graph is discontinuous while V-r graph is continuous
Reason: According to Gauss's theorem only the charge inside a closed surface ca produce electric field at some point.AIf both assertion and reason are ture and reason is the correct explanation of assertion.BIf both assertin and reason are ture but reason is not the correct explanation of assertion .CIf assertion is true but reason is false.DIf both assertion and reason are false.
We can shield a charge from electric fields by putting it inside a hollow conductor. Can we shield a body from the gravitational influence of nearby matter by putting it inside a hollw sphere or by some other means ?
View SolutionA block of mass m is lying at a distance r from a spherical shell of mass m and radius r, then :
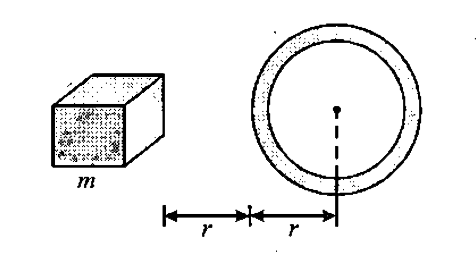
A. only gravitational field inside the shell is zero
B. gravitational field and gravitational potential both are zero inside the shell
C. gravitational potential as well as gravitational field inside the shell are not zero .
D. can't be ascertained
View SolutionSTATEMENT -1 : Gravitational field inside a spherical mass shell is zero even if the mass distribution is uniform or non-uniform.
and
STATEMENT -2 : A mass object when placed inside a mass spherical shell, is protected from the gravitational field of another mass object placed outside the shell.
View SolutionSTATEMENT-1 : Inside an isolated hollow spherical shell of charge, electrostatic potential is constant everywhere
and
STATEMENT-2 : Electric field inside a hollow spherical shell of charge is always zero.
View SolutionAssertion: In case of charged spherical shells, E-r graph is discontinuous while V-r graph is continuous
Reason: According to Gauss's theorem only the charge inside a closed surface can produce electric field at some point.
View SolutionA: A metallic shield in the form of a hollow shell may be built to block an electric field.
R: In a hollow spherical shield, the electric field inside it is zero at every point.
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the center of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
(b) Is the electric field intensity inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape ? Explain.
View Solution
