Two metallic spheres of radii 1cm and 2cm are given charges 10−2C and 5×10−2C respectively. If they are connected by a conducting wire, the final charge on the smaller sphere is
3×10−2C
4×10−2C
1×10−2C
2×10−2C
The correct Answer is:A
To solve the problem of finding the final charge on the smaller sphere after connecting two metallic spheres with given charges, we can follow these steps:
Step 1: Identify the given values
- Radius of the smaller sphere, r1=1cm=0.01m
- Radius of the larger sphere, r2=2cm=0.02m
- Initial charge on the smaller sphere, q1=10−2C
- Initial charge on the larger sphere, q2=5×10−2C
Step 2: Understand the concept of potential
When two conducting spheres are connected by a wire, they reach the same electric potential. The potential V of a sphere is given by the formula:
V=k⋅qr
where k is Coulomb's constant, q is the charge, and r is the radius of the sphere.
Step 3: Set up the equation for equal potentials
Since the potentials of both spheres must be equal after connecting them:
V1=V2
This gives us:
k⋅q′1r1=k⋅q′2r2
Here, q′1 and q′2 are the final charges on the smaller and larger spheres, respectively. The k cancels out:
q′1r1=q′2r2
Step 4: Relate the charges
From the above equation, we can express q′2 in terms of q′1:
q′2=r2r1⋅q′1=21⋅q′1=2q′1
Step 5: Apply the conservation of charge
According to the law of conservation of charge:
q1+q2=q′1+q′2
Substituting the known values:
10−2+5×10−2=q′1+2q′1
This simplifies to:
6×10−2=3q′1
Step 6: Solve for q′1
Now, we can solve for q′1:
q′1=6×10−23=2×10−2C
Final Answer
The final charge on the smaller sphere is:
2×10−2C
---
- Radius of the smaller sphere, r1=1cm=0.01m
- Radius of the larger sphere, r2=2cm=0.02m
- Initial charge on the smaller sphere, q1=10−2C
- Initial charge on the larger sphere, q2=5×10−2C
When two conducting spheres are connected by a wire, they reach the same electric potential. The potential V of a sphere is given by the formula:
V=k⋅qr
where k is Coulomb's constant, q is the charge, and r is the radius of the sphere.
Since the potentials of both spheres must be equal after connecting them:
V1=V2
This gives us:
k⋅q′1r1=k⋅q′2r2
Here, q′1 and q′2 are the final charges on the smaller and larger spheres, respectively. The k cancels out:
q′1r1=q′2r2
From the above equation, we can express q′2 in terms of q′1:
q′2=r2r1⋅q′1=21⋅q′1=2q′1
According to the law of conservation of charge:
q1+q2=q′1+q′2
Substituting the known values:
10−2+5×10−2=q′1+2q′1
This simplifies to:
6×10−2=3q′1
Now, we can solve for q′1:
q′1=6×10−23=2×10−2C
The final charge on the smaller sphere is:
2×10−2C
Similar Questions
Two metal spheres of radii 0.01 m and 0.02 m are given a charge of 15 mC and 45 mC, respectively. They are then connected by a wire. The final charge on the first is …×10−3C.
View SolutionTwo spheres A and B of radius 4 cm and 6 cm are given charges of 80μCand40μC, respectively. If they are connected by a fine wire, then the amount of charge flowing from one to the other is
View SolutionTwo concentric hollow conducting spheres of radius a and b (b>a) contains charges Qa and Qb respectively. If they are connected by a conducting wire then find out following
(i) Final charges on inner and outer spheres.
(ii) Heat produced during the process.
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionFigure shows two conducting spheres separated by large distance and of radius 2 cm and 3 cm containing charges 10μC and 20μC respectively. When the spheres are connected by a conducting wire then find out following :
(i) Ratio of the final charge.
(ii) Final charge on each sphere.
(iii) Ratio of final charge densities.
(iv) Heat produced during the process.

View SolutionThe sphere of radii 8 cm and 2 cm are cooling. Their temperatures are 127∘C and 527∘C respectively . Find the ratio of energy radiated by them in the same time
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionTwo conducting spheres of radii 6km and 12km each, having the same charge 3×10−8C, are kept very far apart. If the spheres are connected to each other by a conductiong wire, find
i. the direction and amount of charge transferred and
ii. final potential each sphere.
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
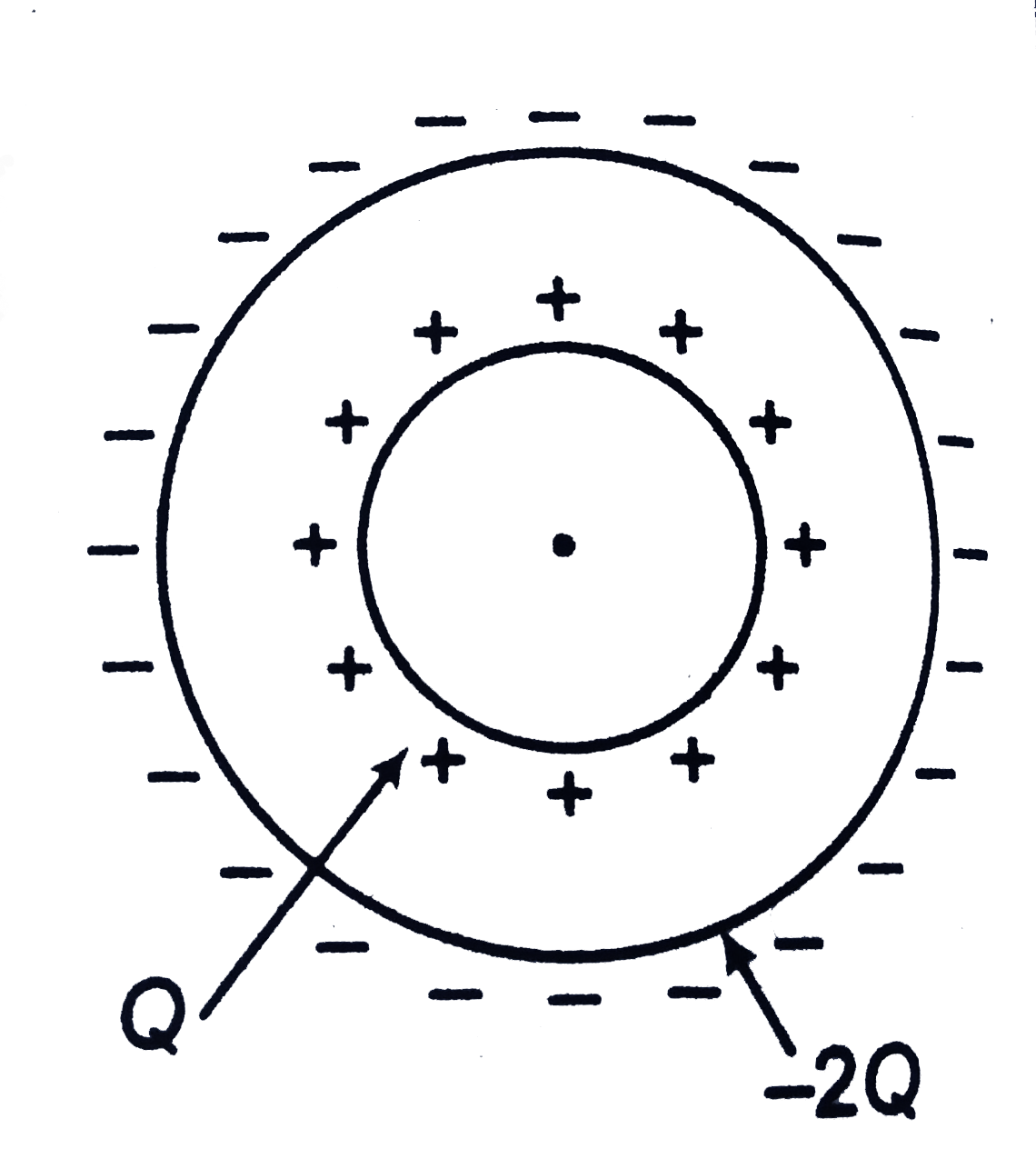
View Solution