The energy stored in a capacitor of capacity C and potential V is given by
The correct Answer is:D
To find the energy stored in a capacitor of capacitance C and potential V, we can follow these steps:
1. Understanding the Capacitor:
A capacitor stores electrical energy in the form of electrostatic potential energy. The capacitance C is defined as the ratio of the charge Q stored on one plate to the potential difference V across the plates:
V=QC
2. Work Done to Charge the Capacitor:
When a small charge dQ is brought to the capacitor, the work done dW in moving this charge against the potential V is given by:
dW=V⋅dQ
3. Substituting for Potential:
Since V=QC, we can substitute this into the work done equation:
dW=(QC)dQ
4. Total Work Done (Energy Stored):
To find the total work done (or energy stored) in the capacitor as we charge it from 0 to Q, we integrate dW:
W=∫Q0dW=∫Q0QCdQ
5. Performing the Integration:
The integral can be computed as follows:
W=1C∫Q0QdQ=1C(Q22)Q0=1C⋅Q22
6. Final Expression for Energy:
Thus, the energy U stored in the capacitor becomes:
U=Q22C
7. Substituting for Charge:
Since Q=CV, we can substitute this into the energy equation:
U=(CV)22C=CV22
8. Conclusion:
Therefore, the energy stored in a capacitor of capacitance C and potential V is given by:
U=12CV2
A capacitor stores electrical energy in the form of electrostatic potential energy. The capacitance C is defined as the ratio of the charge Q stored on one plate to the potential difference V across the plates:
V=QC
When a small charge dQ is brought to the capacitor, the work done dW in moving this charge against the potential V is given by:
dW=V⋅dQ
Since V=QC, we can substitute this into the work done equation:
dW=(QC)dQ
To find the total work done (or energy stored) in the capacitor as we charge it from 0 to Q, we integrate dW:
W=∫Q0dW=∫Q0QCdQ
The integral can be computed as follows:
W=1C∫Q0QdQ=1C(Q22)Q0=1C⋅Q22
Thus, the energy U stored in the capacitor becomes:
U=Q22C
Since Q=CV, we can substitute this into the energy equation:
U=(CV)22C=CV22
Therefore, the energy stored in a capacitor of capacitance C and potential V is given by:
U=12CV2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - B
38 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
The energy stored in 4μF capacitors is
View SolutionFind the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
View SolutionMatch the columns

View SolutionThe energy stored in a capacitor of capacitance 100μF is 50 J. Its potential difference is
View SolutionCalculate the energy stored in the capacitor of capacitance 2μf. The voltmeter gives a reading of 15 V and the ammeter A reads 15mA .
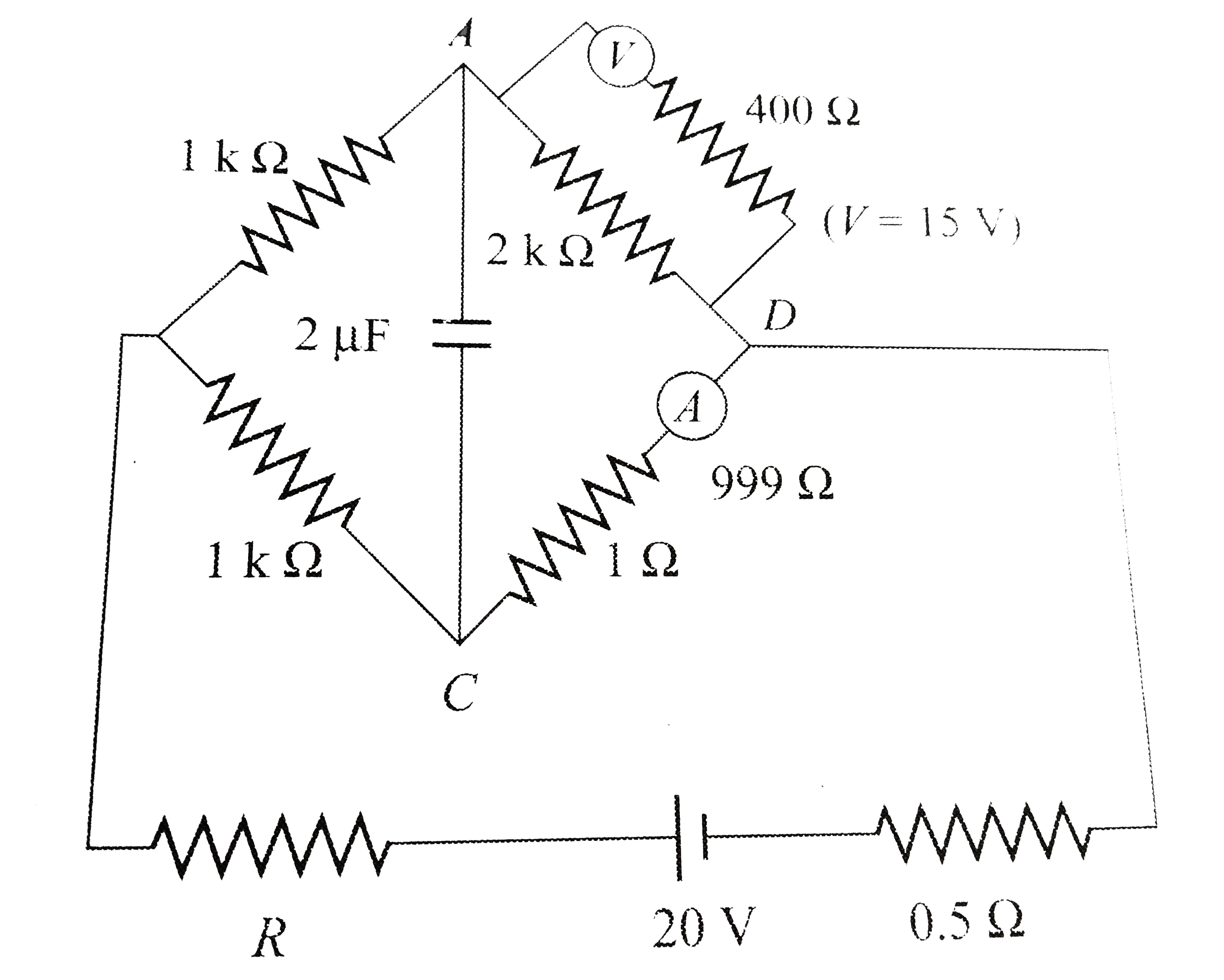
View SolutionIn the ciruit shown in, C=6μF. The charge stored in the capacitor of capacity C is
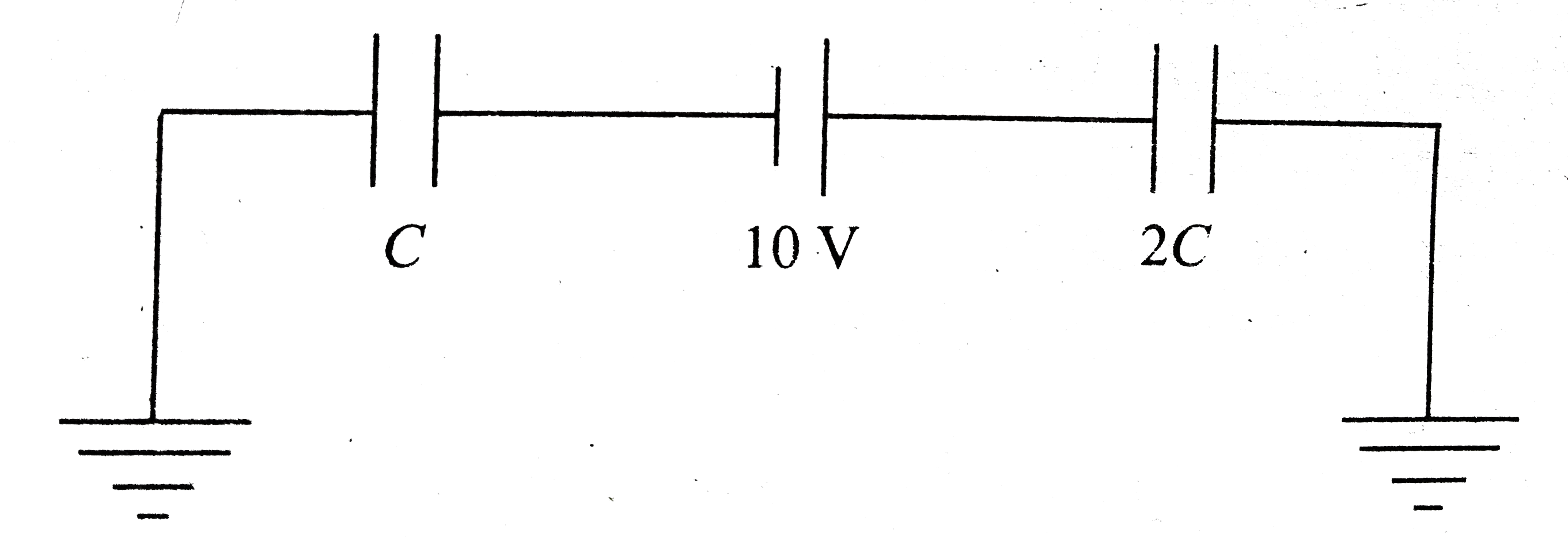 .
.
View SolutionIn the ciruit shown in, C=6μF. The charge stored in the capacitor of capacity C is
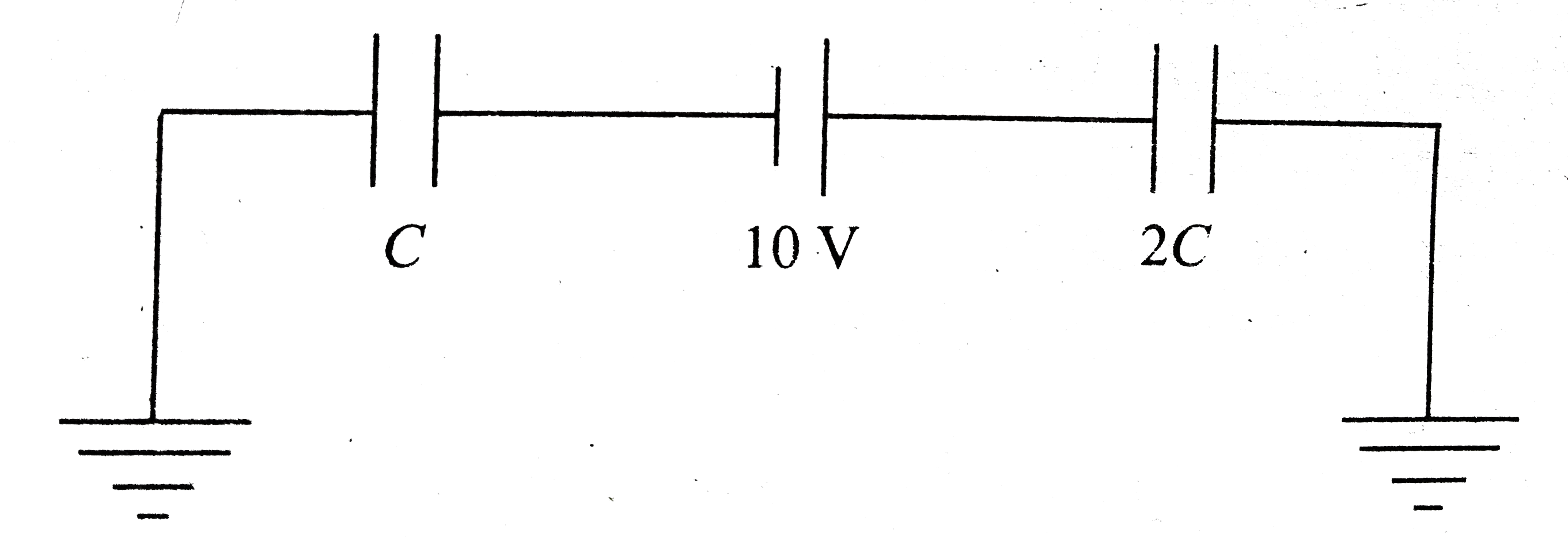 .
.
View SolutionThe energy stored in the capacitor in the steady state is
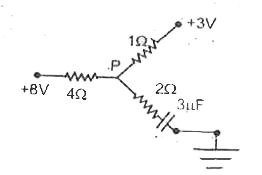
View SolutionSTATEMENT-1 : If the distance plates of a charged isolated capacitor increases, then the potential energy in the electric field of capacitor increases.
and
STATEMENT-2 : The energy stored in a capacitor is always directly proportional to separation between the plates.
View SolutionThree capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emf 6V.
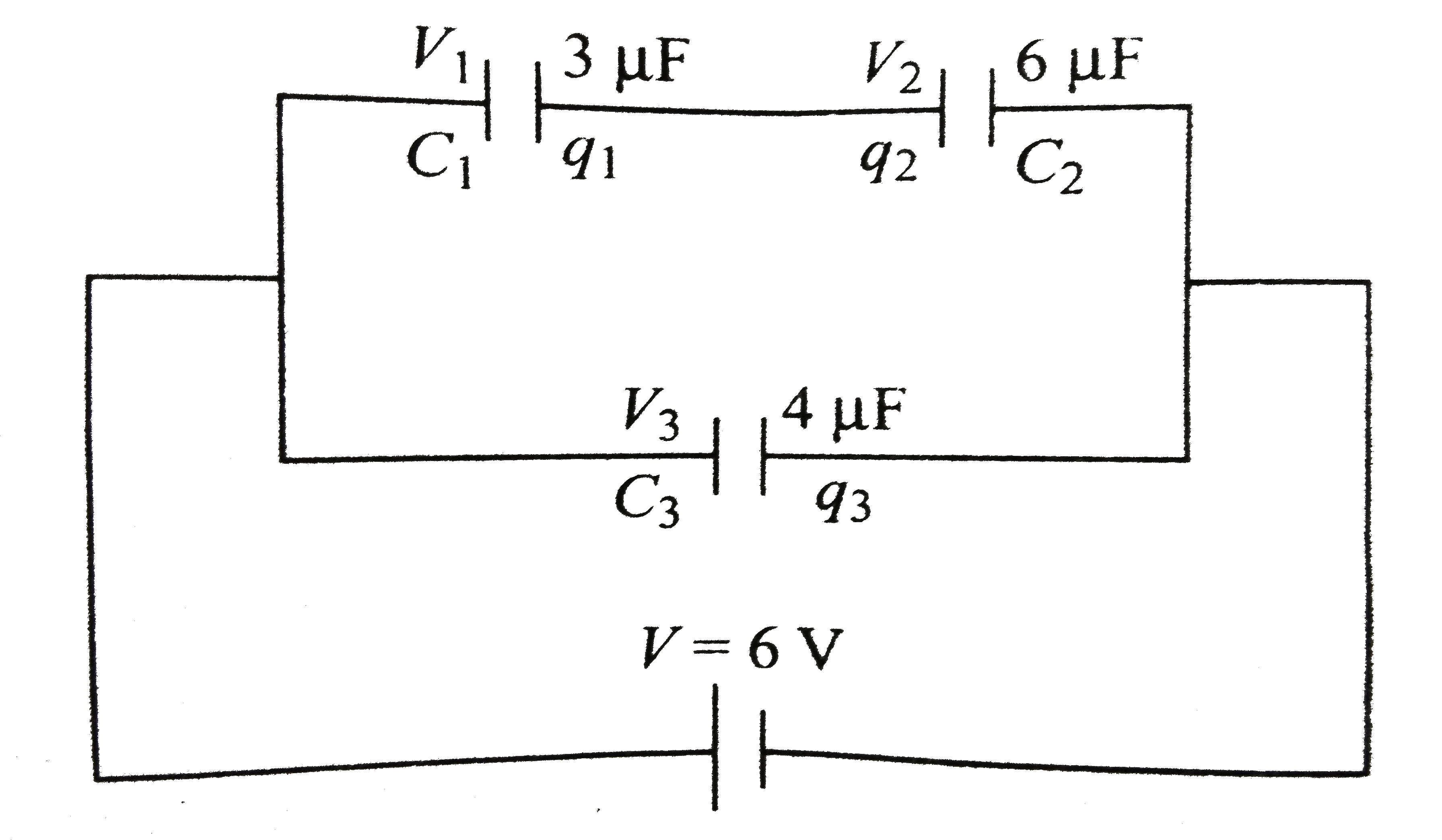 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.
View Solution

