An electric dipole of moment p is palced in the positive of stable equilibrium in uniform electric field of intensity E. It is rotated through an angle θ from the initial position. The potential energy of electric dipole in the final position is
−pE cos θ
pE (1−cosθ)
pE cos θ
pE sin θ
The correct Answer is:A
To find the potential energy of an electric dipole in a uniform electric field after it has been rotated through an angle θ, we can follow these steps:
Step 1: Understand the Initial Position
Initially, the electric dipole (with dipole moment p) is aligned parallel to the electric field E. In this position, the potential energy Ui of the dipole is at its minimum value, which is given by:
Ui=−p⋅E=−pEcos(0)=−pE
Here, the angle between the dipole moment and the electric field is 0∘.
Step 2: Determine the Final Position
After the dipole is rotated through an angle θ, the angle between the dipole moment and the electric field becomes θ.
Step 3: Calculate the Potential Energy in the Final Position
The potential energy Uf of the dipole in the electric field when it makes an angle θ with the field is given by the formula:
Uf=−p⋅E=−pEcos(θ)
This formula arises from the dot product of the dipole moment vector and the electric field vector.
Step 4: Conclusion
Thus, the potential energy of the electric dipole in the final position after being rotated through an angle θ is:
Uf=−pEcos(θ)
Final Answer
The potential energy of the electric dipole in the final position is −pEcos(θ).
---
Initially, the electric dipole (with dipole moment p) is aligned parallel to the electric field E. In this position, the potential energy Ui of the dipole is at its minimum value, which is given by:
Ui=−p⋅E=−pEcos(0)=−pE
Here, the angle between the dipole moment and the electric field is 0∘.
After the dipole is rotated through an angle θ, the angle between the dipole moment and the electric field becomes θ.
The potential energy Uf of the dipole in the electric field when it makes an angle θ with the field is given by the formula:
Uf=−p⋅E=−pEcos(θ)
This formula arises from the dot product of the dipole moment vector and the electric field vector.
Thus, the potential energy of the electric dipole in the final position after being rotated through an angle θ is:
Uf=−pEcos(θ)
The potential energy of the electric dipole in the final position is −pEcos(θ).
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - B
38 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
what is the net force on a dipole in a uniform electric field ?
View SolutionA dipole of electric dipole moment p is placed in a uniform electric field of strength E. If θ is the angle between positive direction of p and E, then the potential energy of the electric dipole is largest when θ is
View SolutionAn electric dipole of dipole moment p is placed in a uniform external electric field E. Then, the
View SolutionAn electric dipole in a uniform electric field experiences (When it is placed at an angle θ with the field)
View SolutionAn electric dipole moment p is placed in an electric field of intensity 'E'. The dipole acquires a position such that the axis of the dipole makes an angle θ with the direction of the field. Assuming that the potential energy of the dipole to be zero when θ=90∘, the torque and the potential energy of the dipole will respectively be
View SolutionAn electric dipole of moment →p is placed normal to the lines of force of electric intensity →E, then the work done in deflecting it through an angle of 180∘ is
View SolutionAt what angle between dipole moment and electric field, electric dipole remains in stable equilibrium in uniform electric field ?
View SolutionThe work in rotating electric dipole of dipole moment p in an electric field E through an angle θ from the direction of electric field, is:
View SolutionAn electric dipole of dipole moment →p is oriented parallel to a unifrom electric field →E, as shown
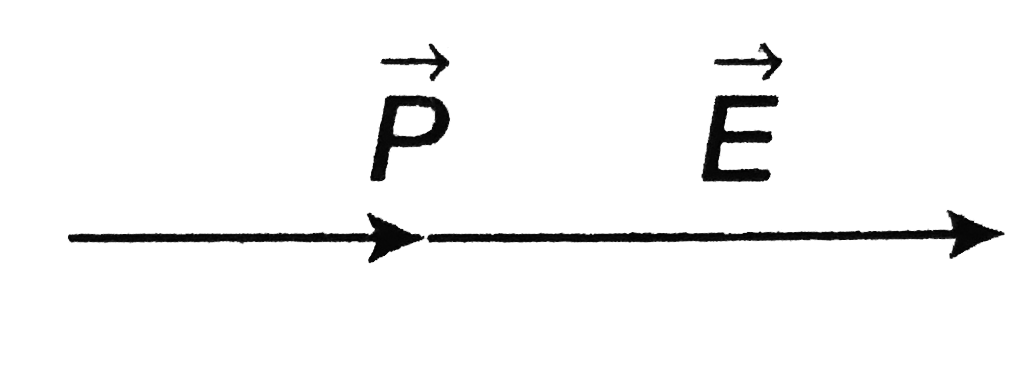
It is rotated to one of four orientations shown below. Rank the final orientations according to the change in the potential energy of the dipole-field system, most negative to most positive.
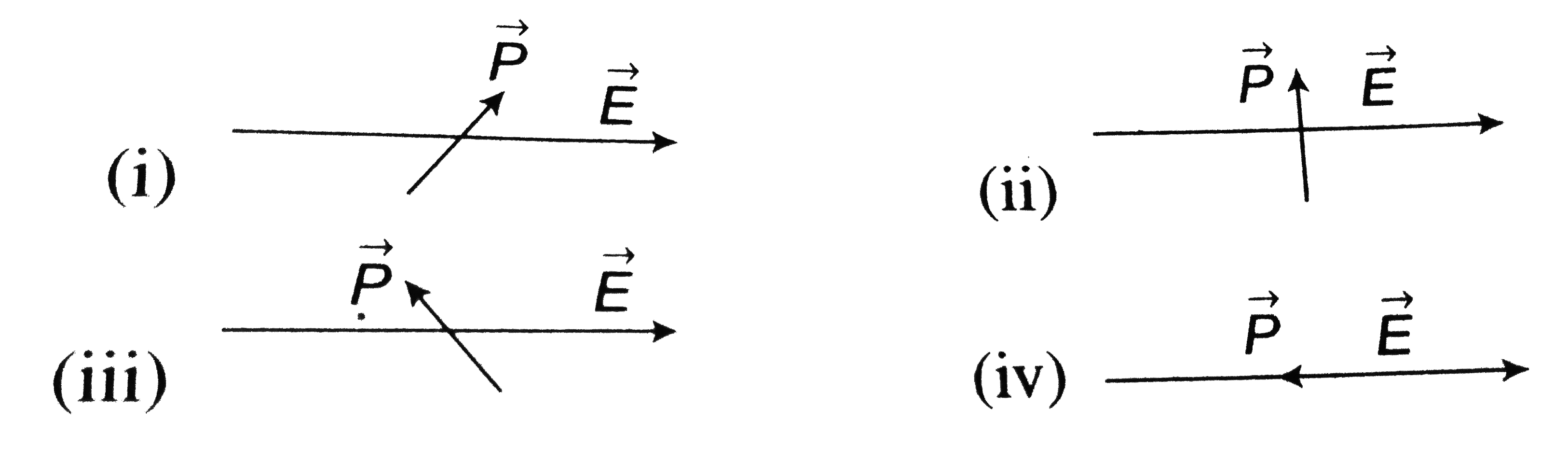
View SolutionAn electric dipole is placed at an angle of 30∘ to a non-uniform electric field. The dipole will experience
View Solution
