A cyclist starts from the centre O of circular path of radius 10 m, covers the radius of circular path and reaches at point X on circumference, then cycles along the semi-circular path and reaches the point Y. If he takes 10 minutes to go from O to Y via X, then the net displacement and average speed of the cyclist would be
Zero,10ms−1
10m,(1+π60)ms−1
10m,(1+π6)ms−1
10m,(1−π60)ms−1
The correct Answer is:B
To solve the problem step-by-step, we will determine the net displacement and average speed of the cyclist as described in the question.
Step 1: Understand the Path Taken by the Cyclist
The cyclist starts from the center O of a circular path with a radius of 10 m. He first travels to point X on the circumference of the circle, which is a distance equal to the radius (10 m). Then, he cycles along the semicircular path to reach point Y.
Step 2: Calculate the Net Displacement
The net displacement is the straight-line distance from the starting point O to the endpoint Y. Since Y is directly opposite to O on the circumference of the circle, the displacement is equal to the radius of the circle.
- Displacement (O to Y) = Radius of the circle = 10 m
Step 3: Calculate the Total Distance Traveled
The total distance traveled by the cyclist consists of two parts:
1. Distance from O to X (which is the radius of the circle).
2. Distance from X to Y (which is the length of the semicircular path).
- Distance OX = 10 m (radius)
- For the semicircular path from X to Y:
- The angle for a semicircle is π radians.
- The arc length (distance from X to Y) can be calculated using the formula:
Arc Length=θ×r
- Here, θ=π and r=10 m.
- Therefore,
Arc Length=π×10=10π m
- Total Distance = Distance OX + Arc Length XY
Total Distance=10+10π m
Step 4: Calculate the Average Speed
The average speed is calculated using the formula:
Average Speed=Total DistanceTotal Time
- The total time taken is given as 10 minutes, which we convert to seconds:
Total Time=10×60=600 seconds
- Now substituting the values into the average speed formula:
Average Speed=10+10π600
- Simplifying this gives:
Average Speed=10(1+π)600=1+π60 m/s
Final Results
- Net Displacement = 10 m
- Average Speed = 1+π60 m/s
The cyclist starts from the center O of a circular path with a radius of 10 m. He first travels to point X on the circumference of the circle, which is a distance equal to the radius (10 m). Then, he cycles along the semicircular path to reach point Y.
The net displacement is the straight-line distance from the starting point O to the endpoint Y. Since Y is directly opposite to O on the circumference of the circle, the displacement is equal to the radius of the circle.
The total distance traveled by the cyclist consists of two parts:
1. Distance from O to X (which is the radius of the circle).
2. Distance from X to Y (which is the length of the semicircular path).
- For the semicircular path from X to Y:
- The angle for a semicircle is π radians.
- The arc length (distance from X to Y) can be calculated using the formula:
Arc Length=θ×r
- Here, θ=π and r=10 m.
- Therefore,
Arc Length=π×10=10π m
Total Distance=10+10π m
The average speed is calculated using the formula:
Average Speed=Total DistanceTotal Time
- The total time taken is given as 10 minutes, which we convert to seconds:
Total Time=10×60=600 seconds
Average Speed=10+10π600
- Simplifying this gives:
Average Speed=10(1+π)600=1+π60 m/s
- Net Displacement = 10 m
- Average Speed = 1+π60 m/s
Topper's Solved these Questions
Similar Questions
A cyclist starts from the centre O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the PQ cicumference and returns to the centre along OQ as shown in fig. If the round trip taken ten minute, the net displacement and average speed of the cylists (in kilometer and kinetic per hour) is
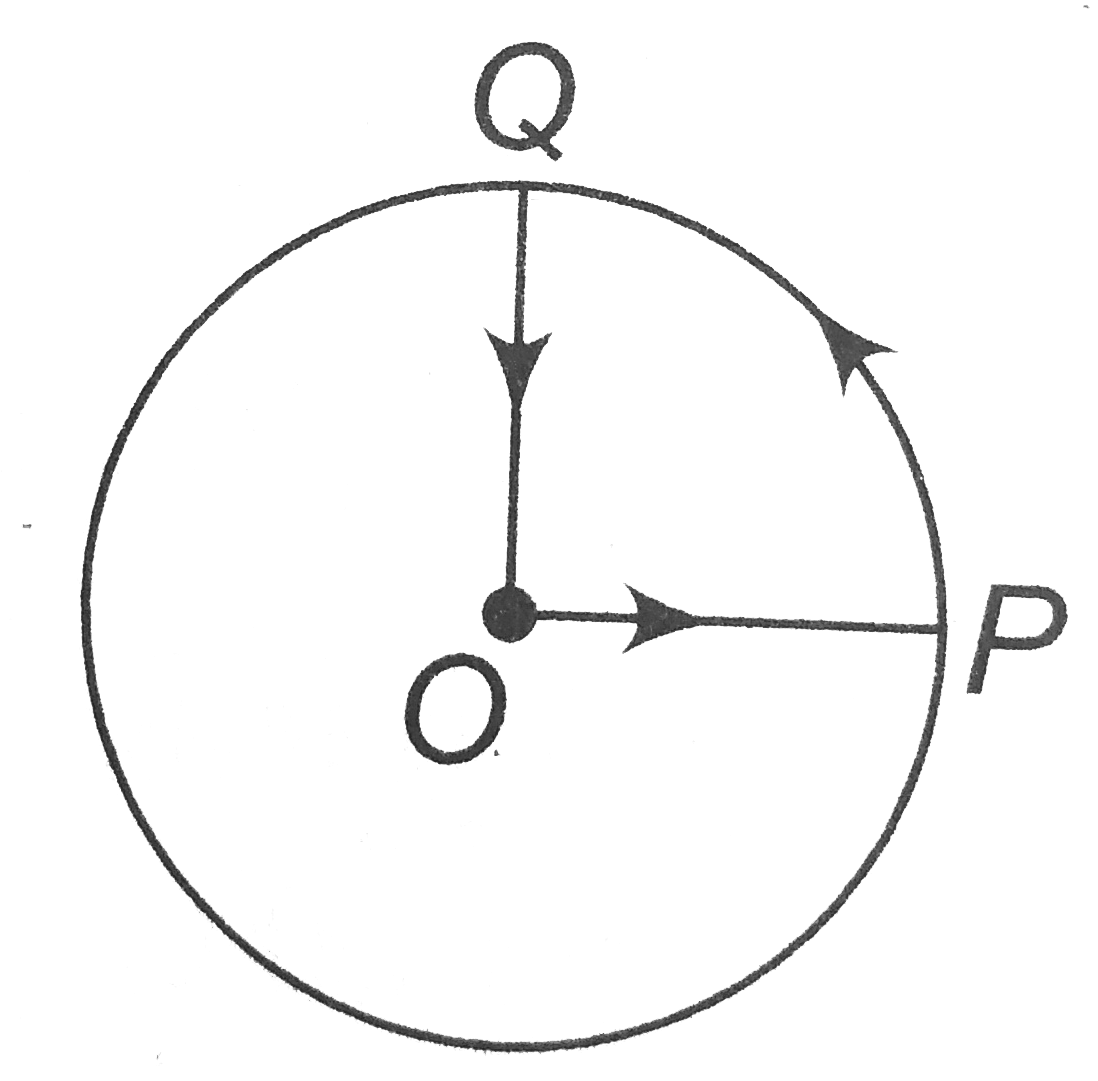
View SolutionA cyclist starts from the center O of a circular park of radius 1km, reaches the edge P of the park, then cycles along the PQ circumference and returns to the center along OQ as shown in fig. If the round trip taken ten minute, the (a) net displacement, (b) average velocity and (c) average speed of the cyclists (in kilometer per hour) is

View SolutionA runner starts from O and goes to O following path OQRO in 1 hr What is net displacement and averages speed?

View SolutionA particle is moving on a circular path of radius 10m with uniform speed of 4ms−1.The magnitude of change in velocity of particle when it completes a semi circular path is
View SolutionA vehicle starts from centre O of a circular park of radius 1 km and reaches point A. After travelling 1/4th of the circumference along AB, he returns to the centre of the park. If the total time taken is 10 minute.

(i) Net displacement
(ii) Average velocity
(iii) Average speed in the round trip
(iv) Magnitude of average velocity in the interval when vehicle moves from A to B, considering motion of the vehicle uniform.
View SolutionA cyclist starts form centre O of a circular park of radius 1km and moves along the path OPRQO as shown in the figure . If he maintains constant speed of 10ms−1, what is his acceleration at point (R )in magnitude and direction ?
 .
.
View SolutionA person runs along a circular path of radius 5 m. Find the magnitude of the displacement if he runs all the way around the circle ?
View SolutionA cyclist starts form centre O of a circular park of radius 1km and moves along the path OPRQO as shown Fig. 2 (EP).15. If he maintains constant speed of 10ms−1, what is his acceleration at point (R )in magnitude and direction ?
 .
.
View SolutionA person runs along a circular path of radius 5 m. If he completes half of the circle find the magnitude of the displacement vector, How far the person ran ?
View SolutionIf a cyclist takes one minute to complete half revolution on a circular path 120 m radius. What is the average velocity?
View Solution
