A person runs along a circular path of radius 5 m. If he completes half of the circle find the magnitude of the displacement vector, How far the person ran ?
10 m, 5π m
5πm, 10 m
5π m , 19m
14 m, 17 m
The correct Answer is:A
To solve the problem, we need to find two things: the magnitude of the displacement vector and the distance the person ran along the circular path.
1. Understanding the Circular Path:
- The radius of the circular path is given as r=5 meters.
- The person completes half of the circle.
2. Finding the Displacement Vector:
- When the person runs from point A to point B (which are endpoints of a diameter of the circle), the displacement vector →AB is the straight line connecting these two points.
- The length of the displacement vector is equal to the diameter of the circle.
- The diameter d can be calculated using the formula:
d=2×r=2×5m=10m
- Thus, the magnitude of the displacement vector is 10m.
3. Finding the Distance Ran:
- The distance the person ran is half of the circumference of the circle.
- The circumference C of a circle is given by:
C=2πr
- Therefore, half of the circumference is:
Distance ran=12C=12×2πr=πr
- Substituting the value of r:
Distance ran=π×5m=5πm
Final Answers:
- The magnitude of the displacement vector is 10m.
- The distance the person ran is 5πm.
- The radius of the circular path is given as r=5 meters.
- The person completes half of the circle.
- When the person runs from point A to point B (which are endpoints of a diameter of the circle), the displacement vector →AB is the straight line connecting these two points.
- The length of the displacement vector is equal to the diameter of the circle.
- The diameter d can be calculated using the formula:
d=2×r=2×5m=10m
- Thus, the magnitude of the displacement vector is 10m.
- The distance the person ran is half of the circumference of the circle.
- The circumference C of a circle is given by:
C=2πr
- Therefore, half of the circumference is:
Distance ran=12C=12×2πr=πr
- Substituting the value of r:
Distance ran=π×5m=5πm
- The magnitude of the displacement vector is 10m.
- The distance the person ran is 5πm.
Similar Questions
A person runs along a circular path of radius 5 m. Find the magnitude of the displacement if he runs all the way around the circle ?
View SolutionA particle is moving in a circular path of radius r. The displacement after half a circle would be
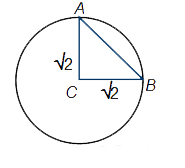
View SolutionA man starts running with constant speed along a circular path of radius √2m He completes two rounds in 16 seconds. The magnitude of the average velocity in first 2 seconds is
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
View SolutionA cyclist is moving with a constant acceleration of 1.2 m/s2 on a straight track. A racer is moving on a circular path of radius 150 m at constant speed of 15 m/s. Find the magnitude of velocity of racer which is measured by the cyclist has reached a speed of 20 m/s for the position represented in the figure -

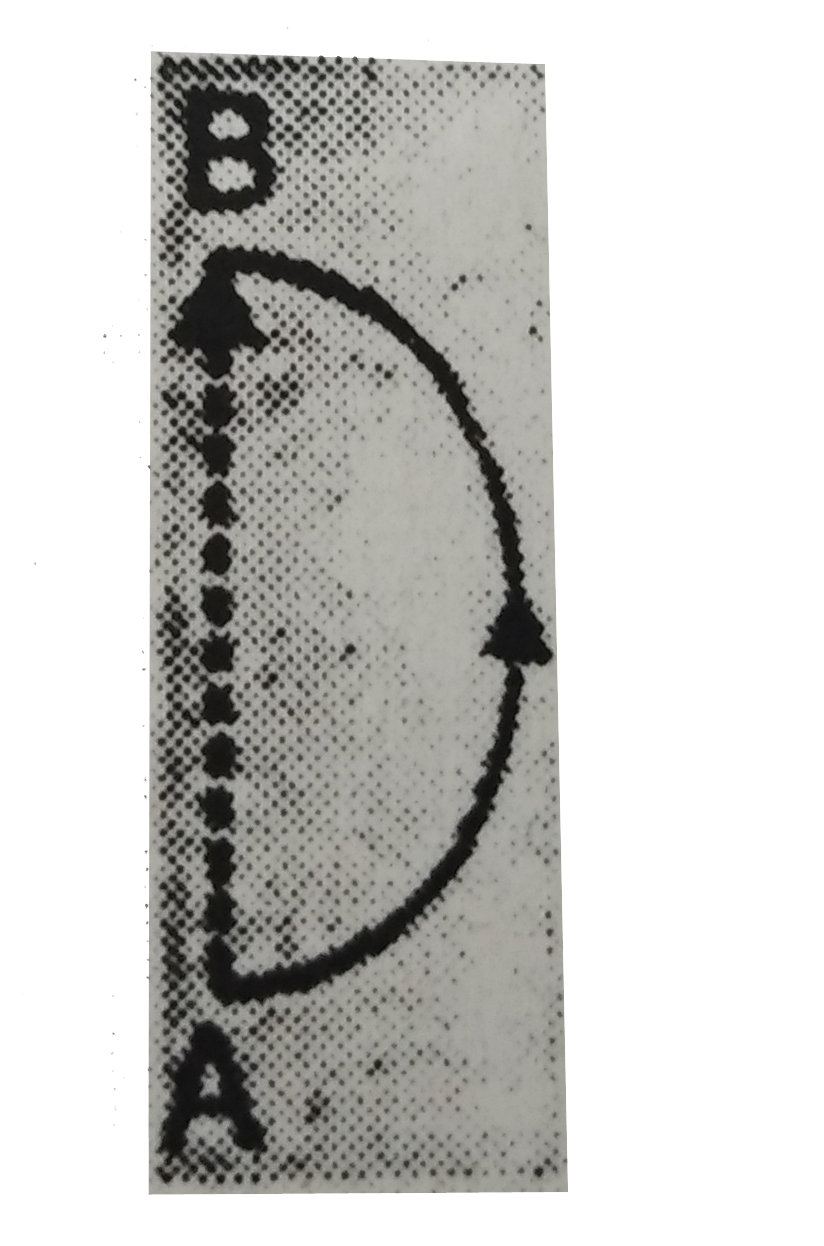
View SolutionA person moves on a semicircular track of radius 40 m. If he starts at one end of the track and reaches the other end, find the distance covered and magnitude of displacement of the person.
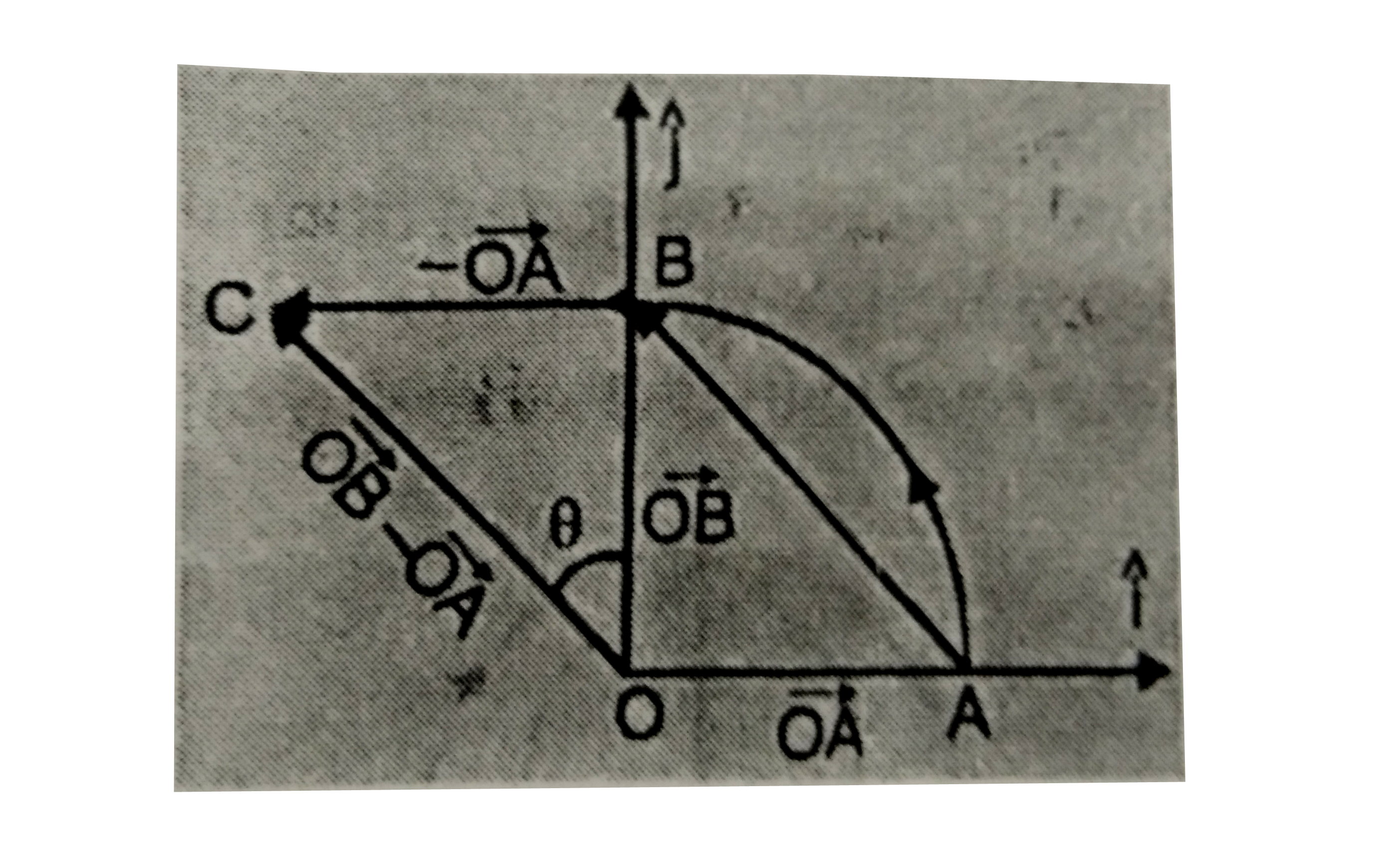
View SolutionA particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?
View SolutionA particle is moving on a circular path of radius 10m with uniform speed of 4ms−1.The magnitude of change in velocity of particle when it completes a semi circular path is
View Solution
A ball of mass m and radius r rolls along a circular path of radius R its speed at the bottom (θ=0∘) of the path is v0 find the force of the path on the ball as a function of θ.
View SolutionA body moves along a circular path of radius 5m. The coefficient of friction between the surface of the path and the body is 0.5. The angular velocity in rad/s with which the body should move so that it does not leave the path is (g−10m/s−2)
View Solution
