An object is subjected to retardation, dvdt=−5√v , which has initial velocity of 4ms−1. The time taken by the object to come to rest would be
2 s
54s
45s
12s
The correct Answer is:C
To solve the problem step by step, we start with the given equation of motion:
1. Write the equation of retardation:
dvdt=−5√v
2. Rearrange the equation:
We can separate the variables by rearranging the equation:
dv√v=−5dt
3. Integrate both sides:
We will integrate the left side from the initial velocity v=4m/s to the final velocity v=0m/s, and the right side from t=0 to t:
∫04dv√v=∫t0−5dt
4. Calculate the left side integral:
The integral ∫dv√v is equal to 2√v:
(2√v)04=2√0−2√4=0−4=−4
5. Calculate the right side integral:
The integral ∫−5dt is equal to −5t:
(−5t)t0=−5t−0=−5t
6. Set the integrals equal to each other:
Now we equate the results from both integrals:
−4=−5t
7. Solve for t:
Rearranging gives:
5t=4⟹t=45 seconds
Thus, the time taken by the object to come to rest is:
t=45 seconds
dvdt=−5√v
We can separate the variables by rearranging the equation:
dv√v=−5dt
We will integrate the left side from the initial velocity v=4m/s to the final velocity v=0m/s, and the right side from t=0 to t:
∫04dv√v=∫t0−5dt
The integral ∫dv√v is equal to 2√v:
(2√v)04=2√0−2√4=0−4=−4
The integral ∫−5dt is equal to −5t:
(−5t)t0=−5t−0=−5t
Now we equate the results from both integrals:
−4=−5t
Rearranging gives:
5t=4⟹t=45 seconds
t=45 seconds
Topper's Solved these Questions
Similar Questions
An object , moving with a speed of 6.25m/s, is decelerated at a rate given by :
dvdt=−2.5√v where v is the instantaneous speed . The time taken by the object , to come to rest , would be :
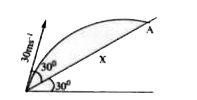
View SolutionAn object in projected up the inclined at the angle shown in the figure with an initial velocity of 30ms−1. The distance x up the incline at which the object lands is
View SolutionA particle is projected from horizontal making an angle of 53∘ with initial velocity 100ms−1. The time taken by the particle to make angle 45∘ from horizontal is
View SolutionAn object Is vertically projected with an initial velocity of 20ms−1.Calculate the distance travelled by the object in 3 seconds.(g=10ms−2)
View SolutionA train is moving with a velocity of 90 km h−1. It is brought to stop by applying the brakes which produce a retardation of 0.5 m s−2? Find : (i) the velocity after 10 s, and (ii) the time taken by the train to come to rest.
View SolutionA particle initially (i.e., at t = 0) moving with a velocity u is subjected to a retarding force, as a result of which it decelerates a=−k√v at a rate where v is the instantaneous velocity and k is a positive constant. The time T taken by the particle to come to rest is given by :
View SolutionA pebble thrown vertically upwards with an initial velocity 50 m s−1 comes to a stop in 5 s. Find the retardation.
View SolutionA ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View SolutionA body of mass 2kg moving on a horizontal surface with an initial velocity of 4ms−1 comes to rest after 2 second. If one wants to keep this body moving on the same surface with a velocity of 4ms−1 the force required is
View SolutionA 0.2kg object at rest is subjected to a force (0.3ˆi−0.4ˆj)N. What is its velocity vector after 6sec
View Solution