A force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
0.5J
2.5J
5J
10 J
The correct Answer is:B
To find the potential energy stored in the spring when a force is applied, we can follow these steps:
1. Identify the Given Values:
- Force (F) = 10 N
- Spring constant (k) = 20 N/m
2. Use Hooke's Law:
Hooke's Law states that the force exerted by a spring is proportional to its displacement (x) and is given by the formula:
F=kx
Here, we can rearrange this formula to find the displacement (x):
x=Fk
3. Calculate the Displacement (x):
Substitute the values of F and k into the equation:
x=10N20N/m=0.5m
4. Calculate the Potential Energy (PE):
The potential energy stored in a compressed or stretched spring is given by the formula:
PE=12kx2
Substitute the values of k and x into the equation:
PE=12×20N/m×(0.5m)2
5. Simplify the Calculation:
Calculate (0.5)2:
(0.5)2=0.25
Now substitute this value back into the equation for potential energy:
PE=12×20×0.25
PE=12×5=2.5J
6. Conclusion:
The potential energy stored in the spring is:
PE=2.5J
- Force (F) = 10 N
- Spring constant (k) = 20 N/m
Hooke's Law states that the force exerted by a spring is proportional to its displacement (x) and is given by the formula:
F=kx
Here, we can rearrange this formula to find the displacement (x):
x=Fk
Substitute the values of F and k into the equation:
x=10N20N/m=0.5m
The potential energy stored in a compressed or stretched spring is given by the formula:
PE=12kx2
Substitute the values of k and x into the equation:
PE=12×20N/m×(0.5m)2
Calculate (0.5)2:
(0.5)2=0.25
Now substitute this value back into the equation for potential energy:
PE=12×20×0.25
PE=12×5=2.5J
The potential energy stored in the spring is:
PE=2.5J
Topper's Solved these Questions
Similar Questions
A rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

View SolutionIn the figure shown, PQ is a uniform sphere of mass M and radius R hinged at point P , with PQ as horizontal diameter. QT is a uniform horizontal rod of mass M and length 2R rigidly attached to the sphere at Q, supported by a vertical spring of spring constant k. If the system is in equilibrium, then the potential energy stored in the spring is
View SolutionA block of mass m held touching the upper end of a light spring of force constant K as shown in figure. Find the maximum potential energy stored in the spring if the block is released suddenly on the spring.

View SolutionTwo masses m and 2m are attached to two ends of an ideal spring as shown in figure. When the spring is in the compressed state, the energy of the spring is 60 J, if the spring is released, then at its natural length

View SolutionA block attached with an ideal spring is kept on a smooth horizontal surface. Now the free end of the spring is pulled with a constant velocity u horizontally. Then the maximum energy stored in the spring and bock system during subsequent motion is :
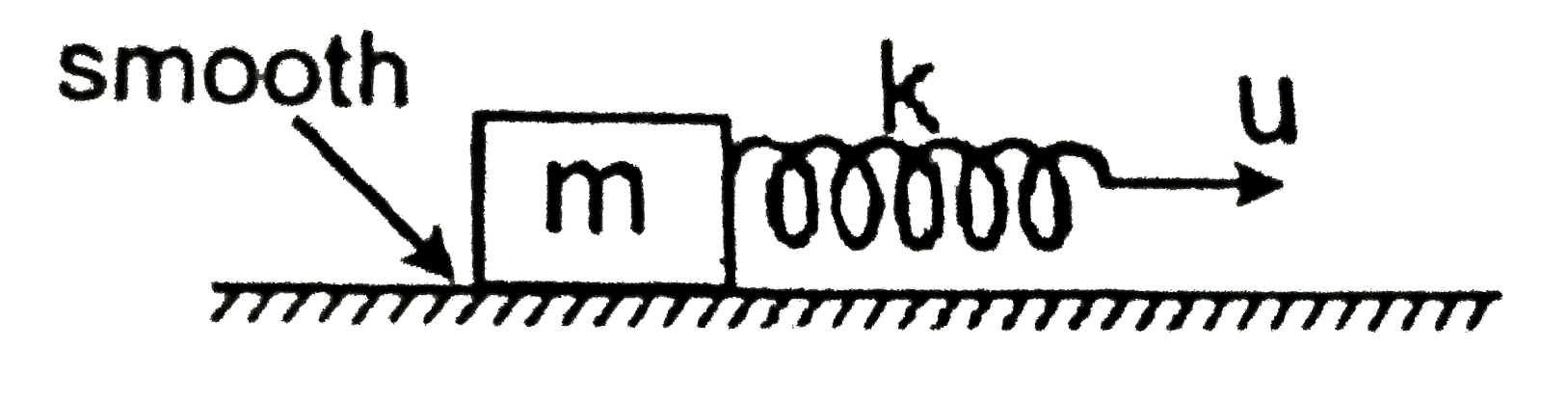
View SolutionDefine spring constant or force constant.
View SolutionA spring of force constant k extends by a length X on loading . If T is the tension in the spring then the energy stored in the spring is
View SolutionThe potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm the potential energy stored in it is:-
View SolutionA long spring when stretched by xcm, has a potential energy U. On increasing the stretching to nxcm, the potential energy stored in spring will be
View SolutionForce constants K1andK2 of two springs are in the ratio 5:4. They are stretched by same length. If potential energy stored in one spring is 25 J then potential energy stored in second spring is
View Solution
