Two masses of 0.25 kg each moves toward each other with speed 3 collide and stick together. Find the final velocity
The correct Answer is:C
To solve the problem of two masses colliding and sticking together, we can use the principle of conservation of linear momentum. Here’s a step-by-step solution:
Step 1: Identify the masses and their velocities
Let:
- Mass of body 1 (m1) = 0.25 kg
- Mass of body 2 (m2) = 0.25 kg
- Velocity of body 1 (v1) = 3 m/s (moving to the right)
- Velocity of body 2 (v2) = -3 m/s (moving to the left, hence negative)
Step 2: Write the equation for conservation of momentum
According to the conservation of momentum:
Initial Momentum=Final Momentum
The initial momentum (p_initial) can be calculated as:
pinitial=m1⋅v1+m2⋅v2
Substituting the values:
pinitial=(0.25kg)⋅(3m/s)+(0.25kg)⋅(−3m/s)
Step 3: Calculate the initial momentum
Calculating the individual terms:
pinitial=0.75kg m/s−0.75kg m/s
pinitial=0kg m/s
Step 4: Set up the equation for final momentum
After the collision, the two masses stick together, so the total mass after the collision is:
mtotal=m1+m2=0.25kg+0.25kg=0.5kg
Let the final velocity after the collision be vf. The final momentum (p_final) is:
pfinal=mtotal⋅vf=0.5kg⋅vf
Step 5: Equate initial and final momentum
Setting the initial momentum equal to the final momentum:
0=0.5kg⋅vf
Step 6: Solve for final velocity
From the equation:
0.5kg⋅vf=0
This implies:
vf=0m/s
Conclusion
The final velocity of the two masses after they collide and stick together is 0 m/s.
---
Let:
- Mass of body 1 (m1) = 0.25 kg
- Mass of body 2 (m2) = 0.25 kg
- Velocity of body 1 (v1) = 3 m/s (moving to the right)
- Velocity of body 2 (v2) = -3 m/s (moving to the left, hence negative)
According to the conservation of momentum:
Initial Momentum=Final Momentum
pinitial=m1⋅v1+m2⋅v2
pinitial=(0.25kg)⋅(3m/s)+(0.25kg)⋅(−3m/s)
Calculating the individual terms:
pinitial=0.75kg m/s−0.75kg m/s
pinitial=0kg m/s
After the collision, the two masses stick together, so the total mass after the collision is:
mtotal=m1+m2=0.25kg+0.25kg=0.5kg
pfinal=mtotal⋅vf=0.5kg⋅vf
Setting the initial momentum equal to the final momentum:
0=0.5kg⋅vf
From the equation:
0.5kg⋅vf=0
This implies:
vf=0m/s
The final velocity of the two masses after they collide and stick together is 0 m/s.
Topper's Solved these Questions
Similar Questions
Two bodies of masses m and 2m are moving along positive x and y axes respectively with equal speed 4ms−1. They collide at origin and stick together. The final velocity of combined mass is
View SolutionTwo bodies of masses 4kg and 2kg are moving towards each other with 3ms−1 and 2ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo bodies of masses 3 kg and 2 kg are moving towards wach other with 3ms−1 and 2ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo bodies of mases 5kg and 3kg are moving towards each other with 2ms−1 and 4ms−1 respectively. Then velocity of centre of mass is
View SolutionTwo men to masses 80kg and 60kg are standing on a wood plank of mass 100kg, that has been placed over a smooth surface. If both the men start moving towards each other with speeds 1m/s and 2m/s respectively then find the velocity of the plank by which it starts moving.
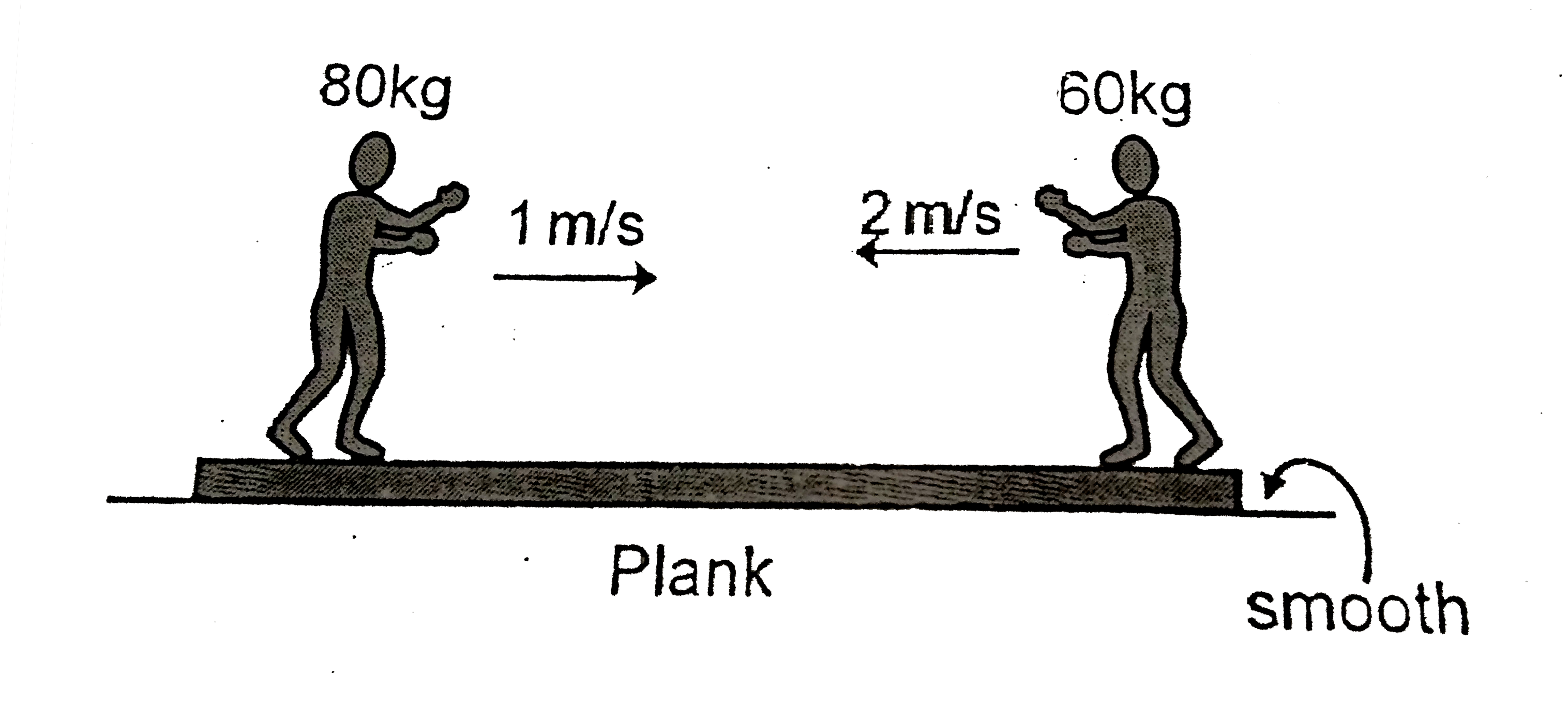
View SolutionTwo objects each of mass 5 kg are moving in the same straight line but in the opposite direction towards each other with some speed of 3 m/s. They stick to each other after collision. What will be the velocity of the combined object after collision?

View SolutionTwo identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View SolutionTwo billiard balls each of mass 0.05 kg moving in opposite directions with speed 6ms−1 collide and rebound with the same speed. What is the impulse imparted to each ball due to the other ?
View SolutionTwo particles A and B of equal size but of masses mkg and 2mkg are moving directly towards each other with speeds 21m/s and 4m/s respectively. After collision, A moves with a speed of 1m/s in the original direction. Then:
View SolutionTwo ice skaters A and B approach each other at right angles. A has mass 30 kg and velocity 1 mis and B has a mass of 20 kg and velocity 2 m/s. They meet and stick together. The final velocity of couple is :
View Solution
