For a spring-mass system spring having spring constant 19.7 N/m is attached to it. What should be the value of mass m (approx.) so that it will give the same period as that of seconds pendulum?
1 kg
2 kg
3 kg
4 kg
The correct Answer is:B
To solve the problem of finding the mass m for a spring-mass system to have the same period as a seconds pendulum, we can follow these steps:
Step 1: Understand the Time Period of the Seconds Pendulum
The time period T of a seconds pendulum is 2 seconds.
Step 2: Write the Formula for the Time Period of a Spring-Mass System
The time period T of a spring-mass system is given by the formula:
T=2π√mk
where:
- m is the mass attached to the spring,
- k is the spring constant.
Step 3: Set the Time Period of the Spring-Mass System Equal to that of the Seconds Pendulum
Since we want the time period of the spring-mass system to be equal to that of the seconds pendulum, we can set:
2π√mk=2
Step 4: Simplify the Equation
Dividing both sides by 2:
π√mk=1
Step 5: Isolate the Square Root
Now, we can isolate the square root:
√mk=1π
Step 6: Square Both Sides
Next, we square both sides to eliminate the square root:
mk=1π2
Step 7: Solve for Mass m
Now, we can solve for mass m:
m=k⋅1π2
Step 8: Substitute the Given Spring Constant
Given that the spring constant k=19.7N/m:
m=19.7⋅1π2
Step 9: Calculate π2
Using the approximation π≈3.14:
π2≈9.86
Step 10: Final Calculation for Mass m
Now substituting π2 into the equation:
m≈19.79.86≈1.997kg
Step 11: Round to the Nearest Whole Number
Rounding 1.997 gives approximately 2kg.
Conclusion
Thus, the mass m that will give the same period as that of a seconds pendulum is approximately 2kg.
The time period T of a seconds pendulum is 2 seconds.
The time period T of a spring-mass system is given by the formula:
T=2π√mk
where:
- m is the mass attached to the spring,
- k is the spring constant.
Since we want the time period of the spring-mass system to be equal to that of the seconds pendulum, we can set:
2π√mk=2
Dividing both sides by 2:
π√mk=1
Now, we can isolate the square root:
√mk=1π
Next, we square both sides to eliminate the square root:
mk=1π2
Now, we can solve for mass m:
m=k⋅1π2
Given that the spring constant k=19.7N/m:
m=19.7⋅1π2
Using the approximation π≈3.14:
π2≈9.86
Now substituting π2 into the equation:
m≈19.79.86≈1.997kg
Rounding 1.997 gives approximately 2kg.
Thus, the mass m that will give the same period as that of a seconds pendulum is approximately 2kg.
Topper's Solved these Questions
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionThe pendulum of a clock is replaced by a spring mass system with the spring having spring constant 0.1Nm−1. What mass should be attached to the spring?
View Solution
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A spring mass system has time period of 2 second. What should be the spring constant of spring if the mass of the block is 10grams ?
View SolutionA student working with a spring mass system finds the values of mass, spring constant and damping constant in CGS unit as 90,4.5×10+3 and 180 respectively. What will be the time period of the spring mass system ?
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be

View SolutionIn the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
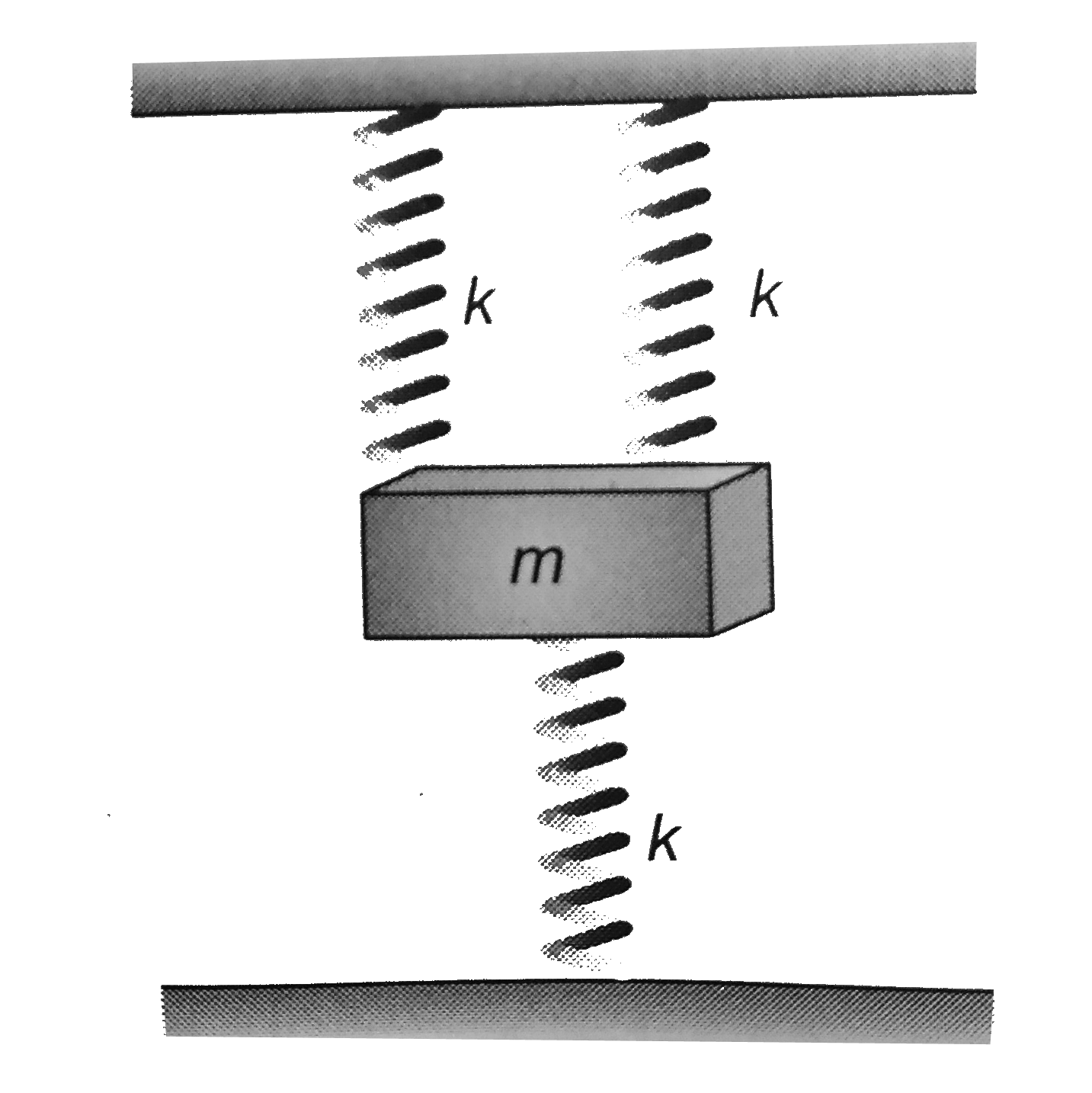
View SolutionIn a spring- mass system , the length of the spring is L, and it has a mass M attached to it and oscillates with an angular frequency ω. The spring is then cut into two parts, one (i) with relaxed length αL and the other (ii) with relaxed length (1−α) L. The force constants of the two spring A and B are
View SolutionThe time period of a spring mass system of spring constant k and mass m is T. Now, the spring is cut into two equal parts and connected in parallel. If the same mass is attached to new arrangement, then new time period is
View Solution
