A uniform solid sphere of mass m and radius R is suspended in vertical plane from a point on its periphery. The time period of its oscillation is
2π√rg
2π√5R3g
2π√7R5g
2π√2R5g
The correct Answer is:C
To find the time period of oscillation of a uniform solid sphere of mass m and radius R suspended from a point on its periphery, we can follow these steps:
Step 1: Understand the System
We have a uniform solid sphere suspended from a point on its surface. This setup acts like a physical pendulum. The time period of a physical pendulum is given by the formula:
T=2π√Imgh
where:
- T is the time period,
- I is the moment of inertia about the pivot point,
- m is the mass of the sphere,
- g is the acceleration due to gravity,
- h is the distance from the pivot to the center of mass of the sphere.
Step 2: Calculate the Moment of Inertia
The moment of inertia I of a solid sphere about its center of mass is given by:
Icm=25mR2
Since we need the moment of inertia about the point on its periphery, we can use the parallel axis theorem:
I=Icm+md2
where d is the distance from the center of mass to the pivot point. For a sphere, d=R (the radius of the sphere). Thus, we have:
I=25mR2+mR2=25mR2+55mR2=75mR2
Step 3: Determine the Distance h
The distance h from the pivot point to the center of mass of the sphere is equal to the radius R:
h=R
Step 4: Substitute Values into the Time Period Formula
Now we can substitute I and h into the time period formula:
T=2π√Imgh=2π
⎷75mR2mgR
Step 5: Simplify the Expression
Now simplify the expression:
T=2π
⎷75Rg=2π√7R5g
Final Answer
Thus, the time period of oscillation of the uniform solid sphere is:
T=2π√7R5g
We have a uniform solid sphere suspended from a point on its surface. This setup acts like a physical pendulum. The time period of a physical pendulum is given by the formula:
- T is the time period,
- I is the moment of inertia about the pivot point,
- m is the mass of the sphere,
- g is the acceleration due to gravity,
- h is the distance from the pivot to the center of mass of the sphere.
The moment of inertia I of a solid sphere about its center of mass is given by:
The distance h from the pivot point to the center of mass of the sphere is equal to the radius R:
Now we can substitute I and h into the time period formula:
⎷75mR2mgR
Now simplify the expression:
⎷75Rg=2π√7R5g
Thus, the time period of oscillation of the uniform solid sphere is:
Topper's Solved these Questions
Similar Questions
A uniform disc of mass m and radius r is suspended through a wire attached to its Centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View SolutionFor a uniform ring of mass M and radius R at its centre
View SolutionA uniform solid sphere of mass m and radius r is suspended symmetrically by a uniform thin spherical shell of radius 2r and mass m.
View SolutionA uniform semi-circular disc of mass m and radius r is suspended as shown in the figure. If T is the time period of small osciallations about an axis passing through point of supension and perpendicular to plane of disk. Then T is equal to
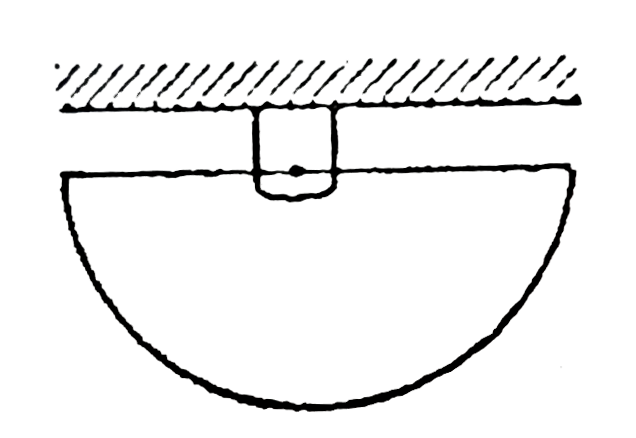
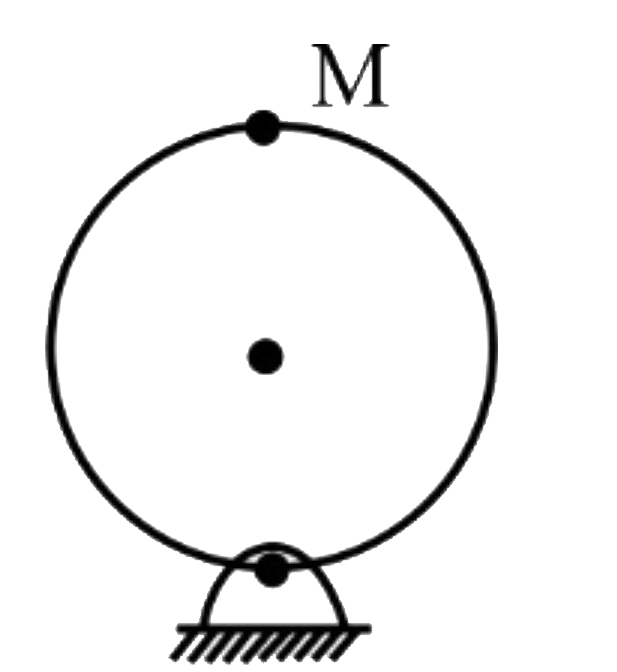
View SolutionA uniform disc of mass M and radius R is supported vertically by a pivot at its periphery as shown. A particle of mass M is fixed to the rim and raised to the highest point above the center. The system is released from rest and it can rotate about pivot freely. The angular speed of the system when the attached object is directly beneath the pivot, is
View SolutionA disc of mass 1 kg and radius 10 cm is suspended by vertical wire at its centre. If the time period is 3.2 s. Find the modulus of torison.
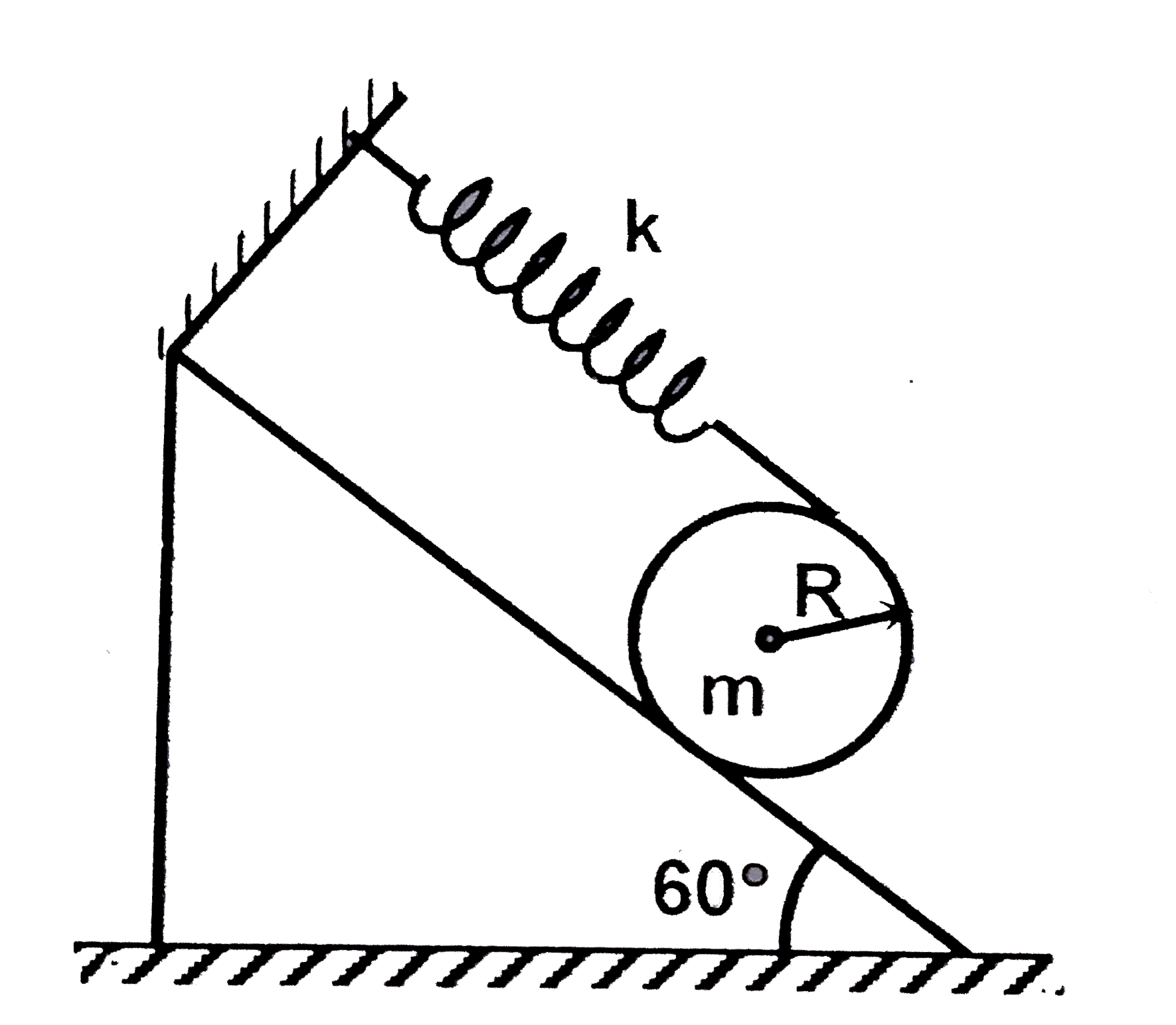
View SolutionA uniform solid sphere of mass 'm' and radius R is in equilibrium on an inclined plane by the action of the light spring of stiffness k, gravity and on it. If the angle of inclination of the plane is 60∘, then find the time period of oscillation for small displancement.
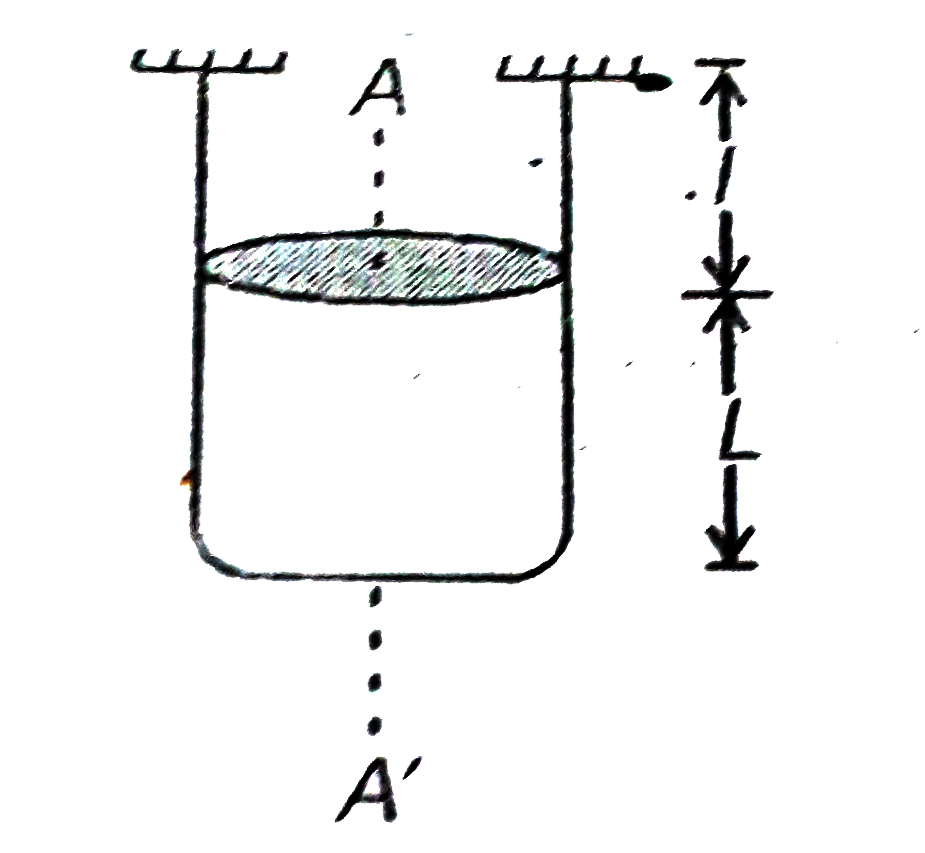
View SolutionA solid cylinder of mass m length L and radius R is suspended by means of two ropes of length l each as shown. Find the time period of small angular oscillations of the cylinder about its axis AA'
View SolutionA ring of radius r is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

View SolutionA ring of radius r is suspended from a point on its circumference. Determine its angular frequency of small oscillations.

View Solution
