Potential of electric ield vector is given by V= 9 (x3−y3), (where , xand y are cartesian Co-ordinates). The electric field strenth vector is
−27x2ˆi+27y2ˆj
27xˆi+27yˆj
27x2yˆi+27xy2ˆj
−27xyˆi+27xyˆj
The correct Answer is:A
To find the electric field strength vector E from the given electric potential V, we can use the relationship between electric potential and electric field. The electric field E is related to the electric potential V by the equation:
E=−∇V
where ∇V is the gradient of the potential V. In Cartesian coordinates, this can be expressed as:
E=−(∂V∂x^i+∂V∂y^j)
Given the potential:
V=9(x3−y3)
we will calculate the partial derivatives with respect to x and y.
Step 1: Calculate ∂V∂x
∂V∂x=∂∂x(9(x3−y3))=9⋅∂∂x(x3)−9⋅∂∂x(y3)
Since y is treated as a constant when differentiating with respect to x:
∂V∂x=9⋅3x2=27x2
Step 2: Calculate ∂V∂y
∂V∂y=∂∂y(9(x3−y3))=9⋅∂∂y(x3)−9⋅∂∂y(y3)
Since x is treated as a constant when differentiating with respect to y:
∂V∂y=−9⋅3y2=−27y2
Step 3: Substitute into the electric field equation
Now we can substitute these derivatives into the equation for the electric field:
E=−(∂V∂x^i+∂V∂y^j)
Substituting the values we found:
E=−(27x2^i−27y2^j)
This simplifies to:
E=−27x2^i+27y2^j
Final Result
Thus, the electric field strength vector is:
E=−27x2^i+27y2^j
---
Topper's Solved these Questions
Similar Questions
The potential at any point is given by V=x(y2−4x2). Calculate the cartesian components of the electric field at the point.
View SolutionThe potential of the electric field produced by point charge at any point (x, y, z) is given by V=3x2+5 , where x ,y are in are in metres and V is in volts. The intensity of the electric field at (-2,1,0) is :
View SolutionElectrostatic field in a region is given by , vecE= (yzhati + zxhatj + xyhatk)V/m , where x,y and z are in m. If electric potential at origin is zero, then potential at (1m,1m, 1m) is
View SolutionA short electric dipoleis placed along y-axis at the origin. The electric field vector at a point P on x-axis is →E1. The dipole is rotated by π2 at its positin . Now, the electric field vector at point P is →E2. Select the correct alternative(s) :
View SolutionThe variation of electric potential for an electric field directed parallel to the x - axis is shown in (Fig. 3.110). Draw the variation of electric field strength with the x- axis.
 .
.
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure. They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V. The value of x for which potential is zero is
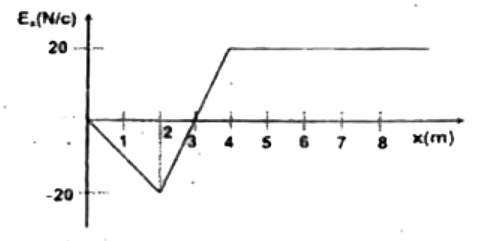
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
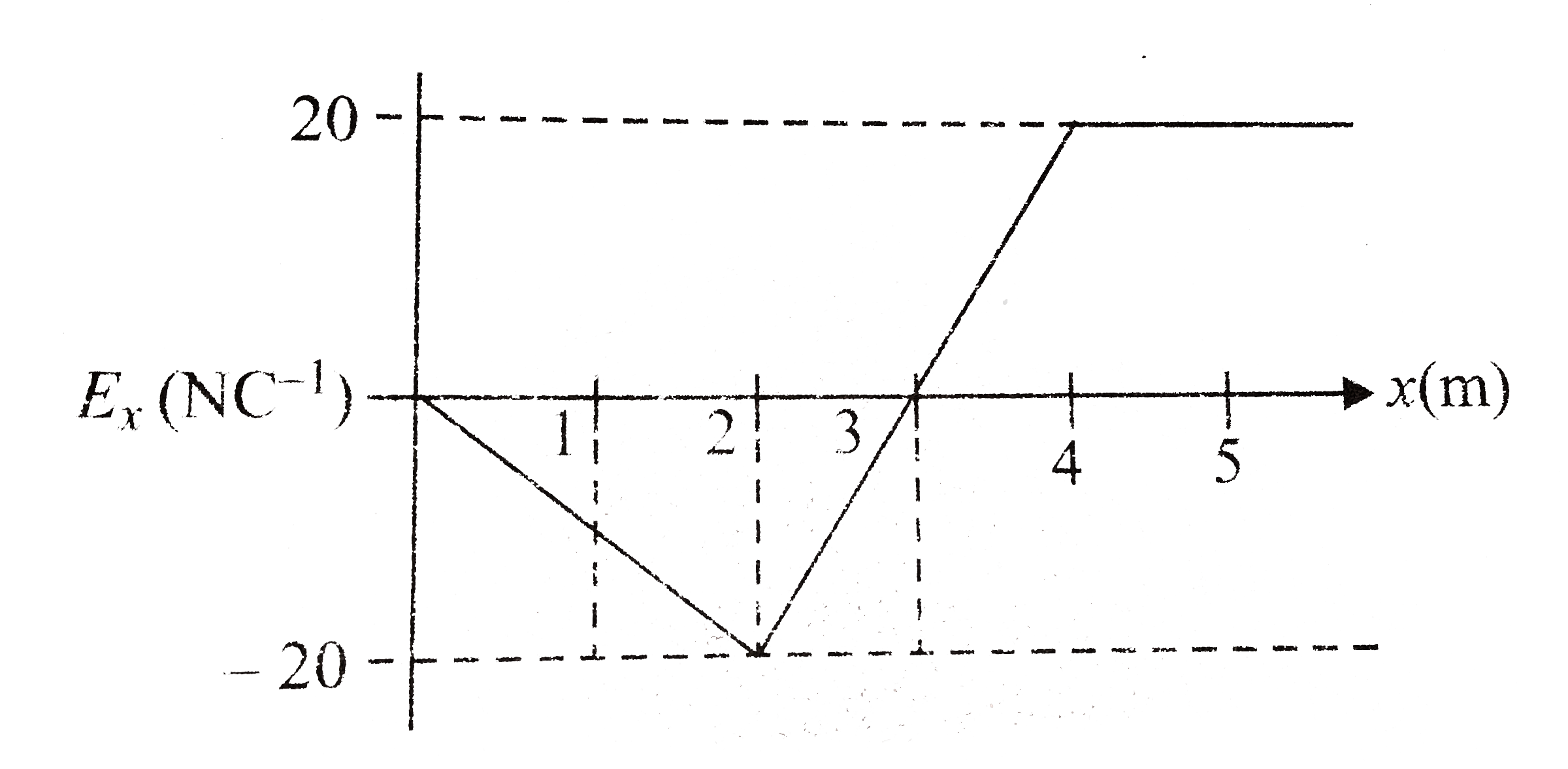
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure.
They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V.
The greatest positive value of electric potential for points of the x-axis for which 0≤x≤6m is
View SolutionElectric potential in a region is varying according to the relation V = 3x22−y24, where x and y are in metre and V is volt, Electric field intensity (in N/C) at a point (1 m, 2 m ) is
View SolutionAssertion: If we see along the axis of a chaged ring, the magnitudeof electric field is minimum at centre and magnitude of electridc potential is maximum.
Reason: Electric field is a vector quantity while electric potential is scalar.
View Solution
