Six charges , q1=+1 μC , q2=+3 μC , q3=+4 μC , q4=−2 μC , q5=−3 μC and q6=−3 μC are placed on a sphee of radius 10 cm. The potential at centre of sphere is
27×105 V
Zero
2.7×105 V
0.27×105V
The correct Answer is:B
To find the electric potential at the center of a sphere with given charges, we can follow these steps:
1. Identify the Charges and Their Values:
- q1=+1μC
- q2=+3μC
- q3=+4μC
- q4=−2μC
- q5=−3μC
- q6=−3μC
2. Understand the Formula for Electric Potential:
The electric potential V due to a point charge is given by:
V=k⋅qr
where k is Coulomb's constant (k≈8.99×109Nm2/C2), q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
3. Determine the Distance:
Since all charges are placed on the surface of a sphere with a radius of 10 cm, the distance r from each charge to the center of the sphere is:
r=0.1m
4. Calculate the Total Potential at the Center:
The total potential at the center Vtotal is the algebraic sum of the potentials due to each charge:
Vtotal=V1+V2+V3+V4+V5+V6
Substituting the values:
Vtotal=k⋅q10.1+k⋅q20.1+k⋅q30.1+k⋅q40.1+k⋅q50.1+k⋅q60.1
5. Factor Out Common Terms:
Since k and 0.1 are common, we can factor them out:
Vtotal=k0.1(q1+q2+q3+q4+q5+q6)
6. Calculate the Sum of Charges:
Now, we calculate the sum of the charges:
qtotal=1μC+3μC+4μC−2μC−3μC−3μC
qtotal=1+3+4−2−3−3=0μC
7. Final Calculation of Potential:
Substituting qtotal=0 into the potential equation:
Vtotal=k0.1⋅0=0V
Conclusion:
The potential at the center of the sphere is:
0V
- q1=+1μC
- q2=+3μC
- q3=+4μC
- q4=−2μC
- q5=−3μC
- q6=−3μC
The electric potential V due to a point charge is given by:
V=k⋅qr
where k is Coulomb's constant (k≈8.99×109Nm2/C2), q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
Since all charges are placed on the surface of a sphere with a radius of 10 cm, the distance r from each charge to the center of the sphere is:
r=0.1m
The total potential at the center Vtotal is the algebraic sum of the potentials due to each charge:
Vtotal=V1+V2+V3+V4+V5+V6
Substituting the values:
Vtotal=k⋅q10.1+k⋅q20.1+k⋅q30.1+k⋅q40.1+k⋅q50.1+k⋅q60.1
Since k and 0.1 are common, we can factor them out:
Vtotal=k0.1(q1+q2+q3+q4+q5+q6)
Now, we calculate the sum of the charges:
qtotal=1μC+3μC+4μC−2μC−3μC−3μC
qtotal=1+3+4−2−3−3=0μC
Substituting qtotal=0 into the potential equation:
Vtotal=k0.1⋅0=0V
The potential at the center of the sphere is:
0V
Topper's Solved these Questions
Similar Questions
Three charges 2 μC , -4 μC and 8 μC are places at the three vertices of an equilateral triangle of side 10 cm. The potential at the centre of triangle is
View SolutionFour point charges qA=2μC,qB=−5μC,qC=2μCandqD=−5μC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1μC placed at the center of the square ?
View SolutionTwo Charges 5 μC and 20 μC are placed on two concentric circes of radius 10 cm and 20 cm respectively lying in x-y plane . The potential at centre is
View SolutionThree charges q1=1μC,q2=−2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. find the net electric force acting on charge q1.
How to proceed Charge q2 will attract charge q1 (along the line joining them) and charge q3 will repel charge q1. Therefore, two forces will act on q1, one due to q2 and another due to q3. Since , the force is a vector quantity both of these force (say F1 and F2) will be added by vector method. Following are two methods of their addition

View SolutionTwo charges +5μC and +10μC are placed 20cm apart. The net electric field at the mid-point between the two charges is
View SolutionThree charges q1=1μC,q2=−2μC,andq3=−1μC are placed at A(0,0,0),B(−1,2,3,)andC(2,−1,1). Find the potential of the system of three charges at P(1,−2,−1).
View SolutionPoint charge q1=2μC and q2=−1μC are kept at points x=0 and x=6 respectively. Electrical potential will be zero at points
View SolutionCondering the situation of the previous question, two experiments wer conducted whose details are as given :
Experiment 1 :Q=10μC
q=50μC
R=15cm
r=10cm
Experiment 2 :Q=20μC
q=60μC
R=15cm
r=10cm
In which case the potential difference between the shells is more ?
View SolutionSuppose that three point charges qa,qb and qc are arranged at the vertices of a right -angled triangle as shown . What is the absolute electric potential at the position of the third charge if qa=−6.0μC,qb=+4.0μC,qc=+2.0μC,a=4.0m and b=3.0 m ? Suppose that the third charge which is initially at rest is repelled to infinity by the combined electric field of the other two charges which are held fixed . What is the final final kinetic energy of the third charge ?
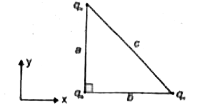
View SolutionIn the circuit shown below C1=10μF, C2=C3=20μF, and C4=40μ F. if the charge on C1 is 20μC then potential difference between X and Y is
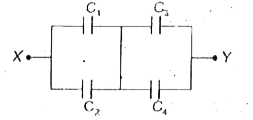
View Solution
