A regular hexagon of side a has a charge Q at each vertex. Potential at the centres of hexagon is (k= (14πε0))
Zero
kQa
12kQa
6kQa
The correct Answer is:D
To find the potential at the center of a regular hexagon with a charge Q at each vertex, we can follow these steps:
1. Understanding the Geometry of the Hexagon:
A regular hexagon has six equal sides and six vertices. The distance from each vertex to the center of the hexagon is the same.
2. Finding the Distance from the Center to a Vertex:
In a regular hexagon with side length a, the distance r from the center of the hexagon to any vertex can be calculated. For a regular hexagon, this distance is given by:
r=a√3⋅2=a√3⋅√3=a
(This can be derived from the properties of the hexagon and the equilateral triangles formed within it.)
3. Calculating the Electric Potential Due to One Charge:
The electric potential V due to a point charge Q at a distance r is given by:
V=kQr
where k=14πϵ0.
4. Calculating the Total Potential at the Center:
Since there are six charges, each contributing equally to the potential at the center, the total potential Vtotal at the center is the sum of the potentials due to each charge:
Vtotal=V1+V2+V3+V4+V5+V6
Since each charge is at the same distance r from the center:
Vtotal=6⋅kQr
Substituting r=a:
Vtotal=6⋅kQa
5. Final Expression for the Potential:
Thus, the potential at the center of the hexagon is:
V=6kQa
Final Answer:
The potential at the center of the hexagon is 6kQa.
---
A regular hexagon has six equal sides and six vertices. The distance from each vertex to the center of the hexagon is the same.
In a regular hexagon with side length a, the distance r from the center of the hexagon to any vertex can be calculated. For a regular hexagon, this distance is given by:
r=a√3⋅2=a√3⋅√3=a
(This can be derived from the properties of the hexagon and the equilateral triangles formed within it.)
The electric potential V due to a point charge Q at a distance r is given by:
V=kQr
where k=14πϵ0.
Since there are six charges, each contributing equally to the potential at the center, the total potential Vtotal at the center is the sum of the potentials due to each charge:
Vtotal=V1+V2+V3+V4+V5+V6
Since each charge is at the same distance r from the center:
Vtotal=6⋅kQr
Substituting r=a:
Vtotal=6⋅kQa
Thus, the potential at the center of the hexagon is:
V=6kQa
The potential at the center of the hexagon is 6kQa.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A hexagon of side 8 cm has a charge 4μC at each of its vertices. The potential at the centre of the hexagon is
A2.7×106VB7.2×1011VC2.5×1012VD3.4×104VSix point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
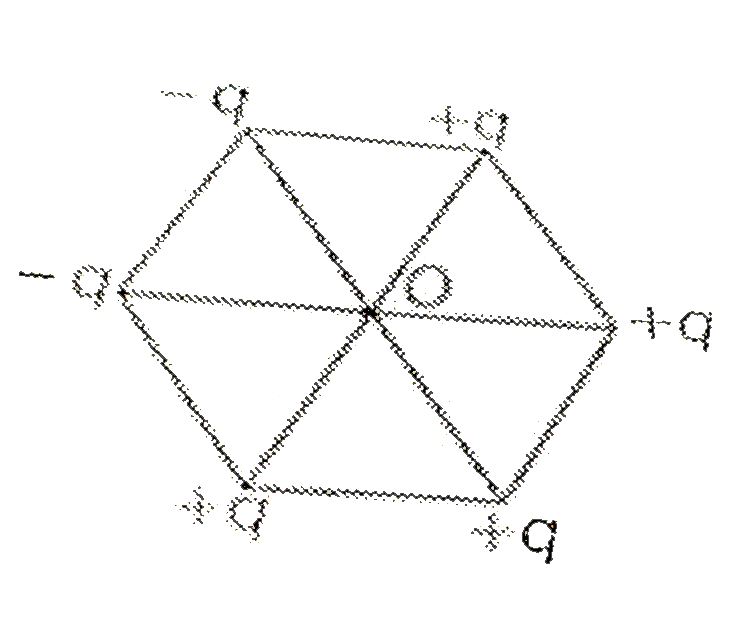
Find the magnitude of electric field at the centre of regular hexagon.A−qB−q6C+1.83qD−1.83q
Assertion : Four point masses each of mass m are placed at points 1, 2, 3 and 6 of a regular hexagon of side a. Then the gravitational field at the centre of hexagon is Gma2
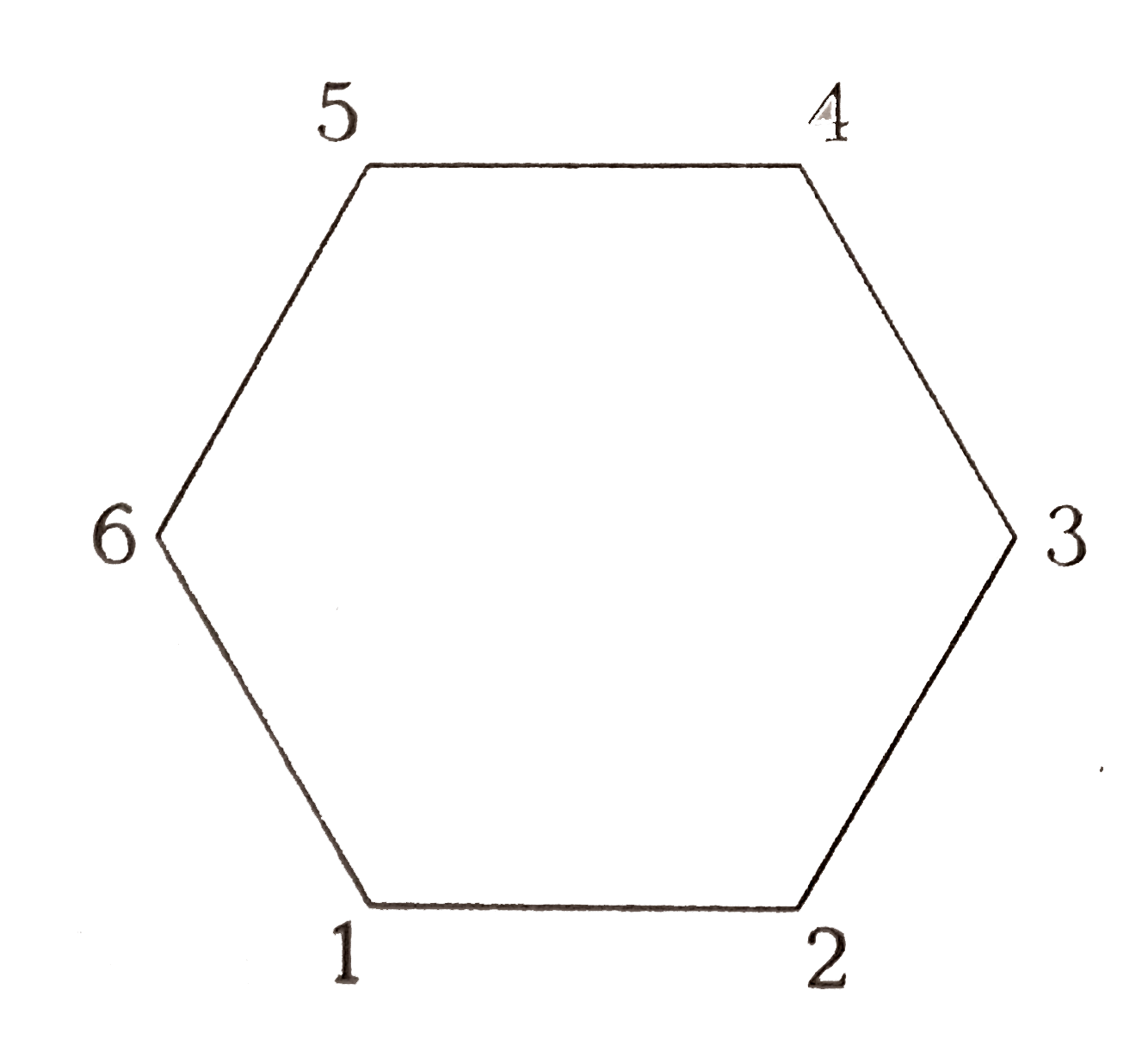
Reason : The field strength due to masses at 3 and 6 are cancelled out.
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionA charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionSix point charges are placed at the vertices of a hexagon of side 1 m as shown in figure. Net electric field at the centre of the hexagon is
View Solution
