A battery of EMF 10 V, with internal resistance 1Ω is being charged by a 120 V d.c. supply using a series resistance of 10Ω. The terminal voltage of the battery is
20 V
10 V
Zero
30 V
The correct Answer is:A
To find the terminal voltage of the battery when it is being charged, we can follow these steps:
Step 1: Identify the components and their values
- EMF of the battery (E) = 10 V
- Internal resistance of the battery (r) = 1 Ω
- External charging supply voltage (V_supply) = 120 V
- Series resistance (R) = 10 Ω
Step 2: Set up the equation using Kirchhoff's Voltage Law (KVL)
When charging the battery, we can apply KVL around the loop:
Vsupply−E−I⋅r−I⋅R=0
Where:
- Vsupply is the external voltage supply (120 V)
- E is the EMF of the battery (10 V)
- I is the current flowing through the circuit
- r is the internal resistance of the battery (1 Ω)
- R is the external resistance (10 Ω)
Step 3: Rearrange the equation
Rearranging the equation gives us:
120−10−I⋅1−I⋅10=0
This simplifies to:
110−11I=0
Step 4: Solve for the current (I)
Now, we can solve for the current I:
11I=110⟹I=11011=10 A
Step 5: Calculate the terminal voltage (V)
The terminal voltage V of the battery while charging can be calculated using the formula:
V=E+I⋅r
Substituting the known values:
V=10+10⋅1=10+10=20 V
Conclusion
The terminal voltage of the battery when being charged is 20 V.
---
- EMF of the battery (E) = 10 V
- Internal resistance of the battery (r) = 1 Ω
- External charging supply voltage (V_supply) = 120 V
- Series resistance (R) = 10 Ω
When charging the battery, we can apply KVL around the loop:
Vsupply−E−I⋅r−I⋅R=0
Where:
- Vsupply is the external voltage supply (120 V)
- E is the EMF of the battery (10 V)
- I is the current flowing through the circuit
- r is the internal resistance of the battery (1 Ω)
- R is the external resistance (10 Ω)
Rearranging the equation gives us:
120−10−I⋅1−I⋅10=0
This simplifies to:
110−11I=0
Now, we can solve for the current I:
11I=110⟹I=11011=10 A
The terminal voltage V of the battery while charging can be calculated using the formula:
V=E+I⋅r
Substituting the known values:
V=10+10⋅1=10+10=20 V
The terminal voltage of the battery when being charged is 20 V.
Topper's Solved these Questions
Similar Questions
A storage battery of emf 8.0 V and internal resistance 0.5Ω is being charged by a 120V dc supply using a series resistor of 15.5Ω. what in the terminal voltage of the battery during charging ? What is the purpose of having a series resistor in the charging circuit?
View SolutionWhat is the amount of work done in bringing a mass from the surface of Earth on one side to a point diametrically opposite on the other side?
View SolutionA battery of six cells each of e.m.f . 2V and internal resistance 0.5Ω is being charged by D.C. mains of e.m.f. 220V by using an external resistance of 10Ω. What is the potential difference across the battery?
View SolutionA battery of six cells each of e.m.f. 2V and internal resistance 0.5Ω is being charged by D.C. mains of e.m.f. 220V by using an external resistance of 10Ω what will be the charging current.
View SolutionA battery of emf 2.0V and internal resistance 0.10Ω is being charged with a current of 5.0A. Find the potential difference between the terminals of the battery?
View SolutionA battery of emf 2.0V and internal resistance 0.10Ω is being charged with a current of 5.0A. Find the potential difference between the terminals of the battery?
View SolutionAn ideal voltmeter V is connected to a 2.0Ω resistor and a battery with emf 5.0V and internal resistance 0.5Ω as shown in figure
(a) What is the current in the 2.0Ω resistor?
(b) What is the terminal voltage of the battery?
(c) What is the reading of the voltmeter?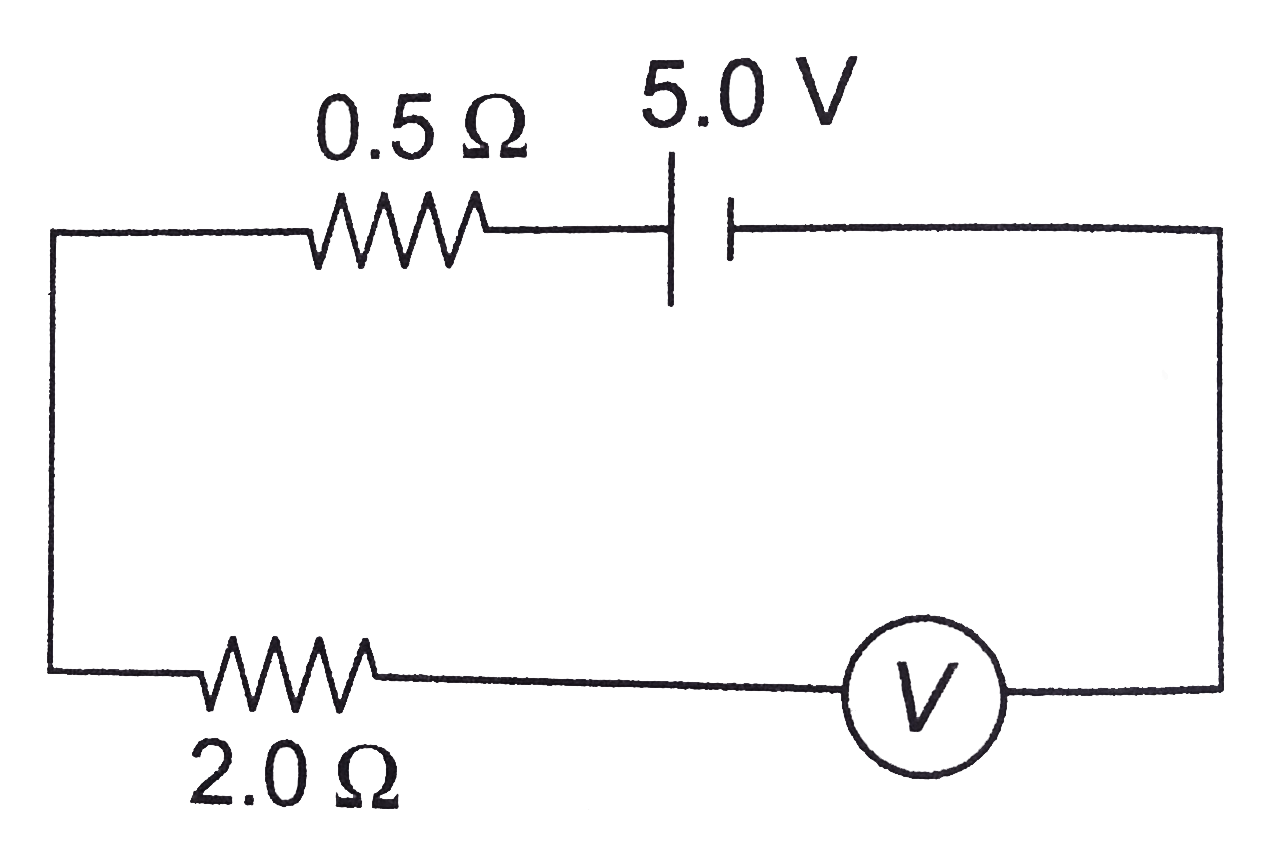
View SolutionA car battery with a 12V e.m.f. and an internal resistance of 0.04Ω is being charged with a current of 50A.
The potential difference V across the terminals of the battery are:
View SolutionA car has a fresh storage battery of emt 12V and internal resistance 5.0×10−2Ω. If the starter moter draws a current of 90A, what is the terminal voltage of the battery when the starter is on?
(b) After long use, the internal resistance of the storange battery increase to 500Ω. What maximum current can be drawn from the battery? Assume the emt of the battery to remain unchanged.
(c) If the discharged battery is changed by an external emf source, is the terminal voltage of the battery during changing greater of less than is emf 12V?
View SolutionA series battery of six cells each of emf2V and internal resistance 0.5Ω is charged by a 100Vdc supply. What resistance should be used in the charging circuit in order to limit the charging current to 8A. Using this relation , obtain (a) the powwer supplied by the dc source, (b) the power dissipated as heat , and (c) the chemical energy stored in the battery in 15min.
View Solution
