Two similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
1:√2
1:2
2:1
√3:1
The correct Answer is:A
To solve the problem, we need to find the ratio of the magnetic field due to one coil to the resultant magnetic field produced by both coils when they are placed mutually perpendicular to each other.
1. Identify the Magnetic Field due to One Coil:
The magnetic field (B1) at the center of a single coil carrying current I is given by the formula:
B1=μ0I2R
where μ0 is the permeability of free space, I is the current, and R is the radius of the coil.
2. Identify the Magnetic Field due to the Second Coil:
Since the second coil is similar and carries the same current, the magnetic field (B2) at the center due to the second coil is also:
B2=μ0I2R
However, B2 is perpendicular to B1.
3. Calculate the Resultant Magnetic Field:
To find the resultant magnetic field (B) when two magnetic fields are perpendicular, we use the Pythagorean theorem:
B=√B21+B22
Substituting the values of B1 and B2:
B=√(μ0I2R)2+(μ0I2R)2
This simplifies to:
B=√2(μ0I2R)2=√2⋅μ0I2R
4. Find the Ratio of the Magnetic Field of One Coil to the Resultant Magnetic Field:
We need to find the ratio of B1 to B:
Ratio=B1B=μ0I2R√2⋅μ0I2R
The μ0I2R terms cancel out:
Ratio=1√2
5. Express the Ratio in Standard Form:
The ratio can be expressed as:
Ratio=1:√2
Final Answer:
The ratio of the magnetic field due to one coil to the resultant magnetic field by both coils is:
1:√2
The magnetic field (B1) at the center of a single coil carrying current I is given by the formula:
B1=μ0I2R
where μ0 is the permeability of free space, I is the current, and R is the radius of the coil.
Since the second coil is similar and carries the same current, the magnetic field (B2) at the center due to the second coil is also:
B2=μ0I2R
However, B2 is perpendicular to B1.
To find the resultant magnetic field (B) when two magnetic fields are perpendicular, we use the Pythagorean theorem:
B=√B21+B22
Substituting the values of B1 and B2:
B=√(μ0I2R)2+(μ0I2R)2
This simplifies to:
B=√2(μ0I2R)2=√2⋅μ0I2R
We need to find the ratio of B1 to B:
Ratio=B1B=μ0I2R√2⋅μ0I2R
The μ0I2R terms cancel out:
Ratio=1√2
The ratio can be expressed as:
Ratio=1:√2
The ratio of the magnetic field due to one coil to the resultant magnetic field by both coils is:
1:√2
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment (Section B) Objective Type Questions (One option is correct)
35 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section C (Objective Type Questions (More than one option are correct)
14 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself
27 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Magnetic Field due to Circular Coil
View SolutionThe magnetic field at the centre of the current carrying coil is
View SolutionTwo coils are having magnetic field B and 2B at their centres and current i and 2i then the ratio of their radius is
View SolutionTwo circular coils made of similar wires but of radii 20 and 40cm are connected in parallel. Find the ratio of the magnetic fields at their centers.
View SolutionTwo circular coils of radii 5.0 cm and 10 cm carry equal currents of 2.0 A. The coils have 50 and 100 turns respectively and are placed in such a way that their planes as well as the centres coincide. Find the magnitude of the magnetic field B at the common centre of the coils if the currents in the coils are (a) in the same sense (b) in the opposite sense.
View SolutionTwo identical coils carry equal currents have a common centre and their planes are at right angles to each other. The ratio of the magnitude of the resulatant magnetic field at the centre and the field due to one coil is
View SolutionThe magnitude of the magnetic field at O ( centre of the circular part ) due to the current - carrying coil as shown is :
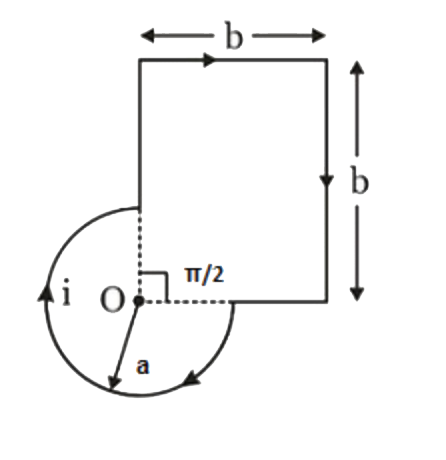
View SolutionIf the planes of two identical concentric coils are perpendicular and the magnetic moment of each coil is M, then the resultant magnetic moment of the two coils wil be
View SolutionDiscuss the similarities between the energy stored in the electric field of charged capacitor and the energy stored in the magnetic field of a current-carrying coil.
View SolutionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is

View Solution
