In an AC circuit, the instantaneous values of e.m.f and current are e=200sin314t volt and i=sin(314t+π3) ampere. The average power consumed in watt is
20 kW
2kW
zero
25kW
The correct Answer is:C
To find the average power consumed in the given AC circuit, we can follow these steps:
Step 1: Identify the given values
We have the following equations for the instantaneous values of e.m.f (E) and current (I):
- e=200sin(314t) volts
- i=sin(314t+π3) amperes
From these equations, we can identify:
- Maximum voltage V0=200 volts
- Maximum current I0=1 ampere
- Phase difference ϕ=π3 radians
Step 2: Calculate RMS values
The root mean square (RMS) values for voltage and current are calculated using the formulas:
- Vrms=V0√2
- Irms=I0√2
Substituting the values:
- Vrms=200√2
- Irms=1√2
Step 3: Calculate the average power
The average power P consumed in an AC circuit can be calculated using the formula:
P=Vrms×Irms×cos(ϕ)
We know:
- cos(ϕ)=cos(π3)=12
Substituting the RMS values and the cosine of the phase difference:
P=(200√2)×(1√2)×12
Step 4: Simplify the expression
Now, simplify the expression:
P=200×12=100
Step 5: Final calculation
Now, we divide by 2 (from the √2 terms):
P=1002=50 watts
Conclusion
The average power consumed in the circuit is 50 watts.
---
We have the following equations for the instantaneous values of e.m.f (E) and current (I):
- e=200sin(314t) volts
- i=sin(314t+π3) amperes
- Maximum voltage V0=200 volts
- Maximum current I0=1 ampere
- Phase difference ϕ=π3 radians
The root mean square (RMS) values for voltage and current are calculated using the formulas:
- Vrms=V0√2
- Irms=I0√2
- Vrms=200√2
- Irms=1√2
The average power P consumed in an AC circuit can be calculated using the formula:
P=Vrms×Irms×cos(ϕ)
- cos(ϕ)=cos(π3)=12
P=(200√2)×(1√2)×12
Now, simplify the expression:
P=200×12=100
Now, we divide by 2 (from the √2 terms):
P=1002=50 watts
The average power consumed in the circuit is 50 watts.
Topper's Solved these Questions
Similar Questions
In an AC circuit the instantaneous values of emf and current are
e=200sin300t volt and i=2sin(300t+π3) amp The average power consumed (in watts) is
View SolutionIn an a.c. circuit, the instantaneous e.m.f. and current are given by e = 100 sin 30 t
i=20sin(30t−π4) In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively :
View SolutionIn an a.c. circuit, the instantaneous e.m.f. and current are given by e = 100 sin 30 t
i=20sin(30t−π4) In one cycle of a.c., the average power consumed by the circuit and the wattless current are, respectively :
View SolutionIn an AC circuit, the applied potential difference and the current flowing are given by
V=20sin100t volt ,I=5sin(100t−π2) amp
The power consumption is equal to
View SolutionThe instantaneous current from an a.c. source is l=5sin(314t) ampere. What are the average and rms values of the current?
View SolutionIn a series LCR circuit, an alternating emf (V) and current (I) are given by the equation V=V0sinωt,I=I0sin(ωt+π3) The average power dissipated in the circuit over a cycle of AC is
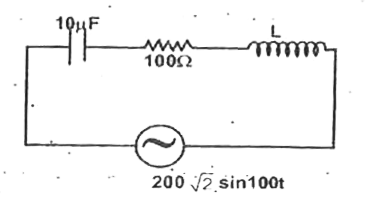
View SolutionA 10 muF capacitor, an inductor and a resistor of 100Omega are connected to an alternating source of emf 200sqrt2 sin 100t as shown in the figure. What is the r.m.s current in the circuit and the value of the inductance if the current and the source voltage attain their maxima simultaneously? What is the average power consumed in this case
View SolutionIn a circuit, the instantaneous values of alternating current and voltages in a circuit is given by
I=1√2sin(100πt)A and
E=1√2sin(100πt+π3)V.
The average power in watts consumed in the circui is
View SolutionIn an AC circuit, V and I are given by V=100sin(100t)vo<s,I=100sin(100t+π3)mA. The power dissipated in circuit is
View SolutionIn an AC circuit, V and I are given by V=100sin(100t)vo<s,I=100sin(100t+π3)mA. The power dissipated in circuit is
View Solution
