When a capacitor is charged then
= conduction current = displacembet current)
in same direction
The correct Answer is:C
To solve the problem regarding the relationship between conduction current Ic and displacement current Id when a capacitor is charged, we can follow these steps:
1. Understanding the Concept: When a capacitor is charged, there are two types of currents involved: conduction current Ic and displacement current Id. The conduction current is the actual flow of charge through the conductor, while the displacement current is related to the changing electric field in the capacitor.
2. Expression for Conduction Current: The conduction current Ic can be expressed in terms of the charge Qt on the capacitor:
Ic=dQtdt
This equation states that the conduction current is the rate of change of charge with respect to time.
3. Expression for Displacement Current: The displacement current Id is defined in terms of the electric flux ΦE:
Id=ϵ0dΦEdt
where ϵ0 is the permittivity of free space.
4. Calculating Electric Flux: The electric flux ΦE due to the electric field E inside the capacitor can be expressed as:
ΦE=E⋅A
where A is the area of the capacitor plates. The electric field E can be expressed in terms of charge density σ:
E=σϵ0=Qt/Aϵ0=Qtϵ0A
Therefore, the electric flux becomes:
ΦE=Qtϵ0⋅A
5. Substituting into Displacement Current: We can substitute the expression for electric flux into the displacement current equation:
Id=ϵ0ddt(Qtϵ0)=dQtdt
Here, ϵ0 cancels out, leading to:
Id=dQtdt
6. Comparing the Two Currents: From the above equations, we see that:
Ic=dQtdtandId=dQtdt
Thus, we conclude that:
Ic=Id
7. Direction of Currents: Since both currents are equal and arise from the same physical process, they flow in the same direction.
8. Final Conclusion: Therefore, the correct statement is:
Ic=Id(both have the same direction)
Ic=dQtdt
This equation states that the conduction current is the rate of change of charge with respect to time.
Id=ϵ0dΦEdt
where ϵ0 is the permittivity of free space.
ΦE=E⋅A
where A is the area of the capacitor plates. The electric field E can be expressed in terms of charge density σ:
E=σϵ0=Qt/Aϵ0=Qtϵ0A
Therefore, the electric flux becomes:
ΦE=Qtϵ0⋅A
Id=ϵ0ddt(Qtϵ0)=dQtdt
Here, ϵ0 cancels out, leading to:
Id=dQtdt
Ic=dQtdtandId=dQtdt
Thus, we conclude that:
Ic=Id
Ic=Id(both have the same direction)
Topper's Solved these Questions
Similar Questions
(A ): When a capacitor is getting charged the conduction current in the connecting wires at any instant is equal to the displacement current in between the capacitor plates. (R) : Conduction current is always greater than the displacement current.
View SolutionA : The displacement current goes through the gap between the plates of a capacitor when the charge on the capacitor does not change.
R : Displacement current arises only when the electric field is constant.
View Solution
Knowledge Check
Assertion : Displacement current goes through the gap between the plates of a capacitor when the charge of the capacitor does not charge
Reason : The displacement current arises in the region in which the electric field is constant with time.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are falseThe conduction current is the same as displacement current when the source is
Aac onlyBdc onlyCeither ac or dcDneither dc nor ac
A capacitor has been charged by ad.c. source. What are the magnitudes of conduction and displacement currents, when it is fully charged?
View SolutionWhen capacitor is fully charged, find current drawn from the cell.
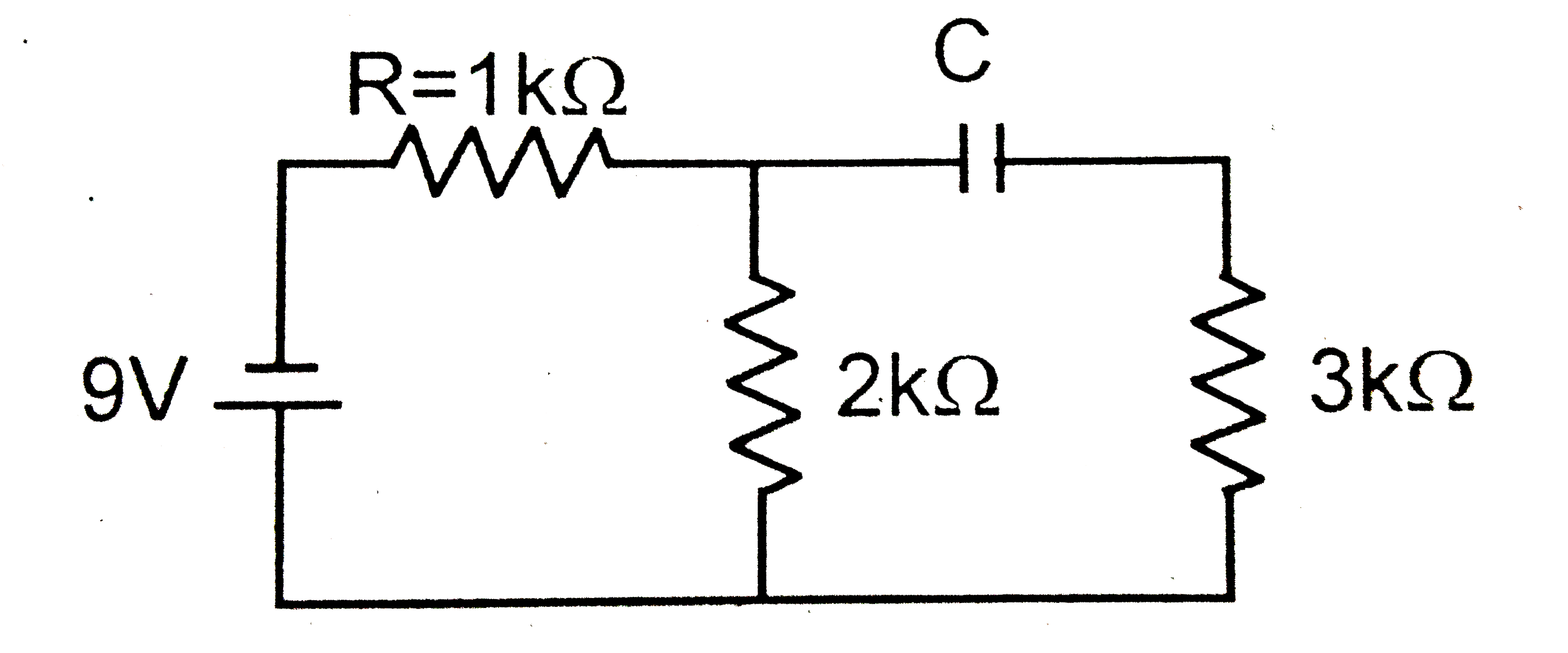
View SolutionA capacitor has been charged by a DC source. What are the magnitude of conduction and displacement current when it is fully charged?
View SolutionThe charging current for a capacitor is 1 A, then the displacement current is
View SolutionA parallel - plate capacitor is being charged.Show that the displacement current across an area in the region between the plates and parallel to it is equal to the conduction current in the connecting wires.
View SolutionA parallel - plate capacitor is being charged.Show that the displacement current across an area in the region between the plates and parallel to it is equal to the conduction current in the connecting wires.
View Solution
