The charging current for a capacitor is 1 A, then the displacement current is
1A
0A
2A
12A
The correct Answer is:A
To solve the problem regarding the displacement current when the charging current for a capacitor is given as 1 A, we can follow these steps:
1. Understanding the Concept:
The displacement current Id is related to the changing electric field in a capacitor. It is defined as:
Id=ϵ0dΦEdt
where ΦE is the electric flux and ϵ0 is the permittivity of free space.
2. Electric Flux Calculation:
The electric flux ΦE through the capacitor is given by:
ΦE=E⋅A
where E is the electric field between the plates and A is the area of the plates. For parallel plates, the angle between the electric field and the area vector is 0 degrees, hence cos(0)=1.
3. Electric Field in a Capacitor:
The electric field E between the plates of a parallel plate capacitor can be expressed as:
E=Qϵ0A
where Q is the charge on the plates.
4. Substituting into Flux:
Substituting the expression for E into the flux equation gives:
ΦE=(Qϵ0A)A=Qϵ0
5. Differentiating the Flux:
Now, we differentiate the electric flux with respect to time:
dΦEdt=ddt(Qϵ0)=1ϵ0dQdt
6. Substituting into Displacement Current:
Now substituting this back into the equation for displacement current:
Id=ϵ0dΦEdt=ϵ0⋅1ϵ0dQdt=dQdt
7. Relating to Conduction Current:
The conduction current Ic is defined as:
Ic=dQdt
Given that the charging current is 1 A, we have:
Ic=1A
8. Final Result:
Therefore, the displacement current Id is equal to the conduction current:
Id=Ic=1A
Conclusion
The displacement current when the charging current for a capacitor is 1 A is also 1 A.
---
The displacement current Id is related to the changing electric field in a capacitor. It is defined as:
Id=ϵ0dΦEdt
where ΦE is the electric flux and ϵ0 is the permittivity of free space.
The electric flux ΦE through the capacitor is given by:
ΦE=E⋅A
where E is the electric field between the plates and A is the area of the plates. For parallel plates, the angle between the electric field and the area vector is 0 degrees, hence cos(0)=1.
The electric field E between the plates of a parallel plate capacitor can be expressed as:
E=Qϵ0A
where Q is the charge on the plates.
Substituting the expression for E into the flux equation gives:
ΦE=(Qϵ0A)A=Qϵ0
Now, we differentiate the electric flux with respect to time:
dΦEdt=ddt(Qϵ0)=1ϵ0dQdt
Now substituting this back into the equation for displacement current:
Id=ϵ0dΦEdt=ϵ0⋅1ϵ0dQdt=dQdt
The conduction current Ic is defined as:
Ic=dQdt
Given that the charging current is 1 A, we have:
Ic=1A
Therefore, the displacement current Id is equal to the conduction current:
Id=Ic=1A
The displacement current when the charging current for a capacitor is 1 A is also 1 A.
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - C Previous Years Questions
22 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - A Objective Type Questions
25 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
Similar Questions
Knowledge Check
Assertion : Displacement current goes through the gap between the plates of a capacitor when the charge of the capacitor does not charge
Reason : The displacement current arises in the region in which the electric field is constant with time.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are false
If potential difference between the plates of capacitor changes with rate of dVdt=106voltsec, and capacitance of capacitors is 1μF, then find displacement current between the plates.
View SolutionA : The displacement current goes through the gap between the plates of a capacitor when the charge on the capacitor does not change.
R : Displacement current arises only when the electric field is constant.
View SolutionA 100Ω resistance and a capacitor of 100Ω reactance are connected in series across a 220 V source. When the capacitor is 50% charged, the peak value of the displacement current is
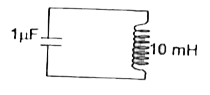
View SolutionIn the given circuit, if initial charge on the capacitor is 100μC, then the maximum current is (Initially, the inductor is fully deenergized)
View SolutionA capacitor, made of two parallel plates each of plate area A and separation d, is being charged by an external ac socurce. Show that the displacement current inside the same as the current charging the capacitor.
View SolutionA capacitor, made of two parallel plates each of plate area A and separation d, is being charged by an external ac socurce. Show that the displacement current inside the same as the current charging the capacitor.
View SolutionA parallel plate capacitor 20 μF is being charged by a voltage source whose potential is changing at the rate of 3 V/s. The conduction current through the connecting wires, and the displacement current through the plates of the capacitor, would be, respectively:
View Solution
