The wavelength of sound waves arriving at P from two coherent sources S1 and S2 is 4 m as shown. While intensity of each wave is I0 the resultant intensity at point P is 2I0 find minimum value of x _PHY_E06_238_Q01.png)
2(√5−2)m
2(√5−1)m
1√+1m
2(√5+2)m
Step by step video & image solution for The wavelength of sound waves arriving at P from two coherent sources S_1 and S_2 is 4 m as shown. While intensity of each wave is I_0 the resultant intensity at point P is 2I_0 find minimum value of x by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In the figure , the intensity of waves arriving at D from two coherent soucrces s1ands2isI0. The wavelength of the wave is λ=4m . Resultant intensity at D will be

View SolutionTwo waves of equal amplitude a from two coherent sources (S1&S2) interfere at a point R such that S2R−S1R=1.5λThe intensity at point R Would be
View Solution
Knowledge Check
In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2
When two waves of intensities l1andl2 coming from coherent sources interfere at a point P, where phase difference is ϕ, then resultant intensity (lres) at point P would be
View SolutionIf the intensity of the waves obvserved by two coherent sources is 1. Then the intensity of resultant waves in constructive interferences will be:
View SolutionTwo sinusoidal waves of intensity I having same frequency and same amplitude interferes constructively at a point. The resultant intensity at a point will be
View SolutionFour monochromatic and coherent sources of light emitting waves in phase at placed on y axis at y = 0, a, 2a and 3a. If the intensity of wave reaching at point P far away on y axis from each of the source is almost the same and equal to I0, then the resultant intensity at P for a=λ8 is nI0. The value of [n] is.
Here [] is greatest integer funciton.
View SolutionTwo incoherent sources of light emitting light of intensity I0 and 3I0 interfere in a medium. Calculate, the resultant intensity at any point.
View SolutionThe intensity of interference waves in an interference pattern is same as I0. The resultant intensity at any point of observation will be
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
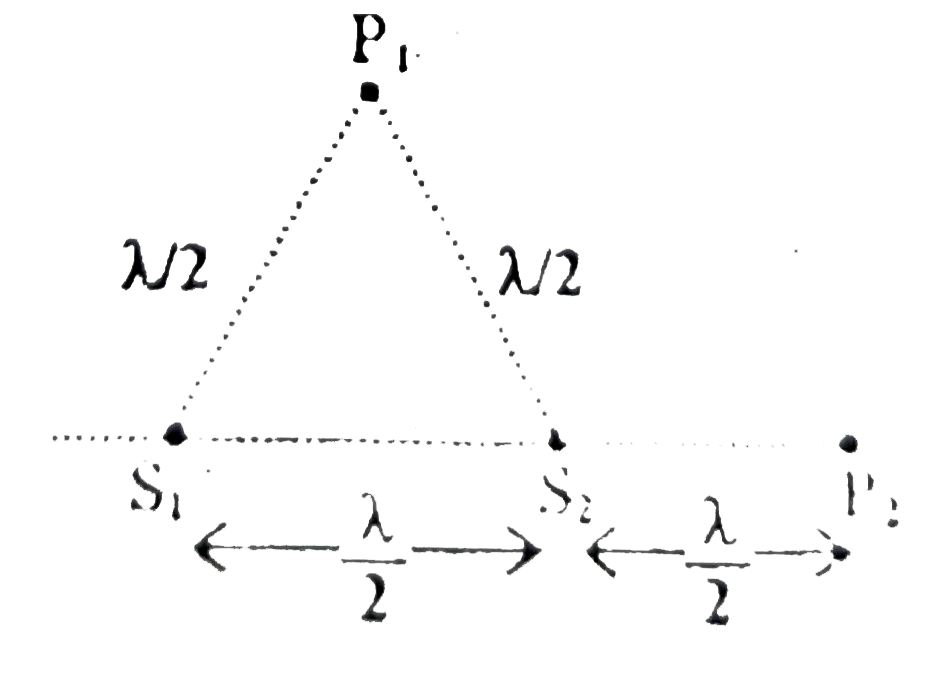
View Solution
