A short electric dipole having dipole moment ¯ρ is placed along x-axis as shown in figure. The electric potential at point A(-2, 3) is (k=14πε0 and all quantities are in S. I. units)
−kP(13)32
−2kP(13)32
−2kP(13)2
2kP(13)2
To solve the problem of finding the electric potential at point A due to a short electric dipole, we can follow these steps:
Step 1: Understand the Configuration
The dipole moment ¯¯¯p is placed along the x-axis, and we need to find the electric potential at point A located at coordinates (-2, 3).
Step 2: Calculate the Distance from the Dipole to Point A
The distance r from the origin (where the dipole is located) to point A can be calculated using the distance formula:
r=√(−2)2+(3)2=√4+9=√13
Step 3: Determine the Angle θ
The angle θ between the dipole moment and the line connecting the dipole to point A can be found using the tangent function:
tanθ=yx=3−2
Thus, we can find sinθ and cosθ:
sinθ=3√13,cosθ=−2√13
Step 4: Use the Formula for Electric Potential Due to a Dipole
The electric potential V at a point due to a dipole is given by:
V=14πϵ0⋅¯¯¯p⋅^rr2
Where ^r is the unit vector in the direction of the position vector from the dipole to the point.
Step 5: Substitute Values into the Formula
The potential due to the dipole at point A can be expressed as:
V=14πϵ0⋅p⋅cosθr2
Substituting cosθ and r:
V=14πϵ0⋅p⋅(−2√13)(√13)2
V=14πϵ0⋅−2p13
Step 6: Final Result
Thus, the electric potential at point A is:
V=−2p13⋅4πϵ0
Step 7: Identify the Correct Option
From the options provided, the correct answer matches:
V=−2kp133/2
where k=14πϵ0.
Summary
The electric potential at point A due to the dipole is:
V=−2kp133/2
The dipole moment ¯¯¯p is placed along the x-axis, and we need to find the electric potential at point A located at coordinates (-2, 3).
The distance r from the origin (where the dipole is located) to point A can be calculated using the distance formula:
r=√(−2)2+(3)2=√4+9=√13
The angle θ between the dipole moment and the line connecting the dipole to point A can be found using the tangent function:
tanθ=yx=3−2
Thus, we can find sinθ and cosθ:
sinθ=3√13,cosθ=−2√13
The electric potential V at a point due to a dipole is given by:
V=14πϵ0⋅¯¯¯p⋅^rr2
Where ^r is the unit vector in the direction of the position vector from the dipole to the point.
The potential due to the dipole at point A can be expressed as:
V=14πϵ0⋅p⋅cosθr2
Substituting cosθ and r:
V=14πϵ0⋅p⋅(−2√13)(√13)2
V=14πϵ0⋅−2p13
Thus, the electric potential at point A is:
V=−2p13⋅4πϵ0
From the options provided, the correct answer matches:
V=−2kp133/2
where k=14πϵ0.
The electric potential at point A due to the dipole is:
V=−2kp133/2
Topper's Solved these Questions
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Try Yourself
63 Videos
- TEST 2BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 2EXERCISE - Exercise
308 Videos
Similar Questions
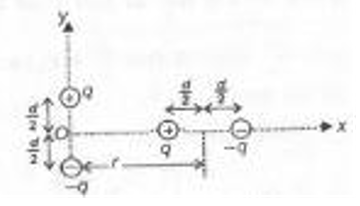
Two identical electric dipoles of dipole moments p are placed as shown in the figure. The electrostatic force on dipole placed along x-axis is (d << r) (14πε0 )
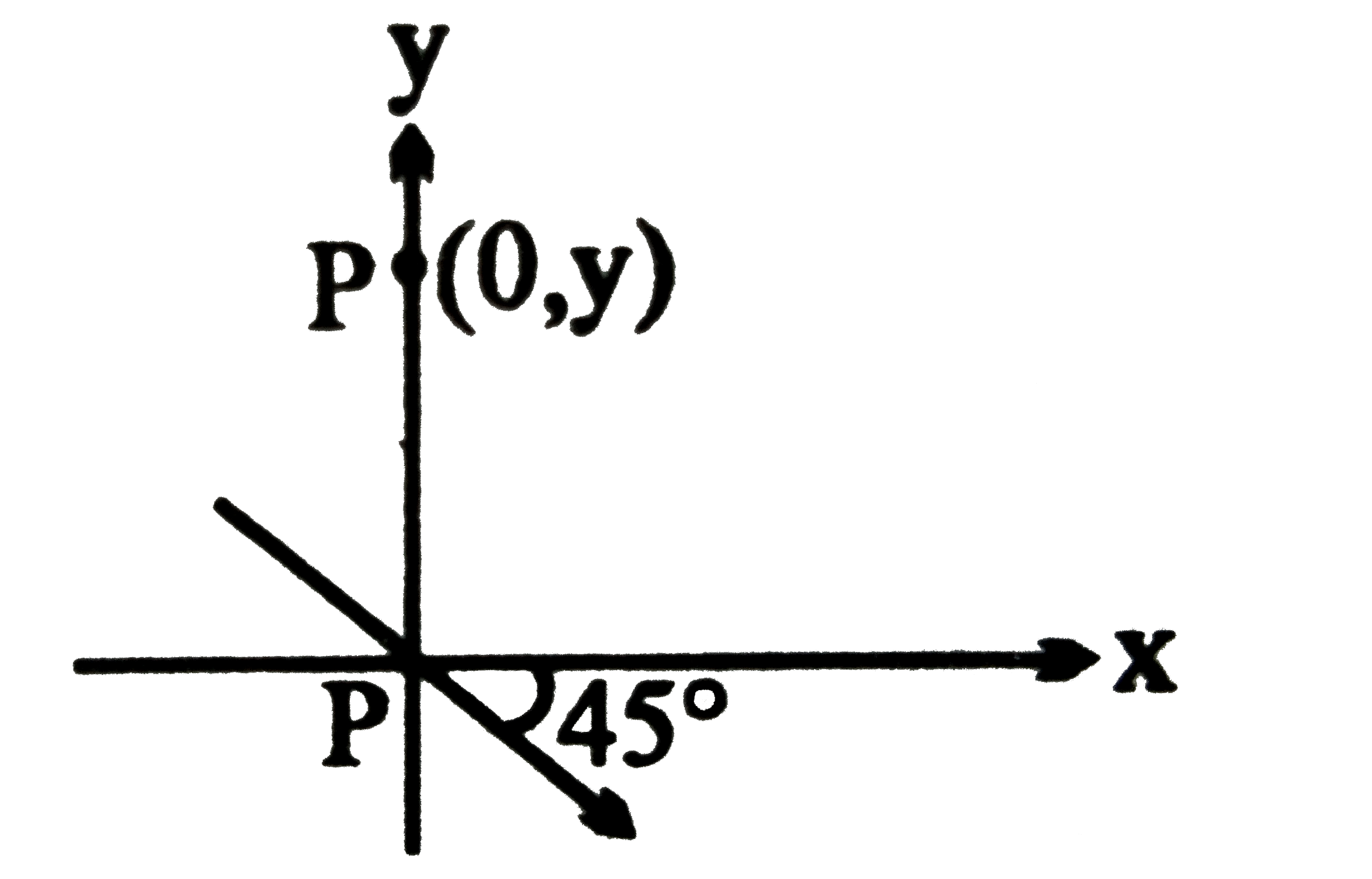
View SolutionA dipole is placed at origin of coordinate system as shown in figure, find the electric field at point P(0,y)
 .
.
View SolutionA small electric dipole is placed at origin with its dipole moment directed along positive x-axis .The direction of electric field at point (2,2√2,0)
View SolutionTwo small electric dipoles each of dipole moment pˆi are situated at (0,0,0) and (r,0,0). The electric potential at a point (r2,√3r2,0) is:
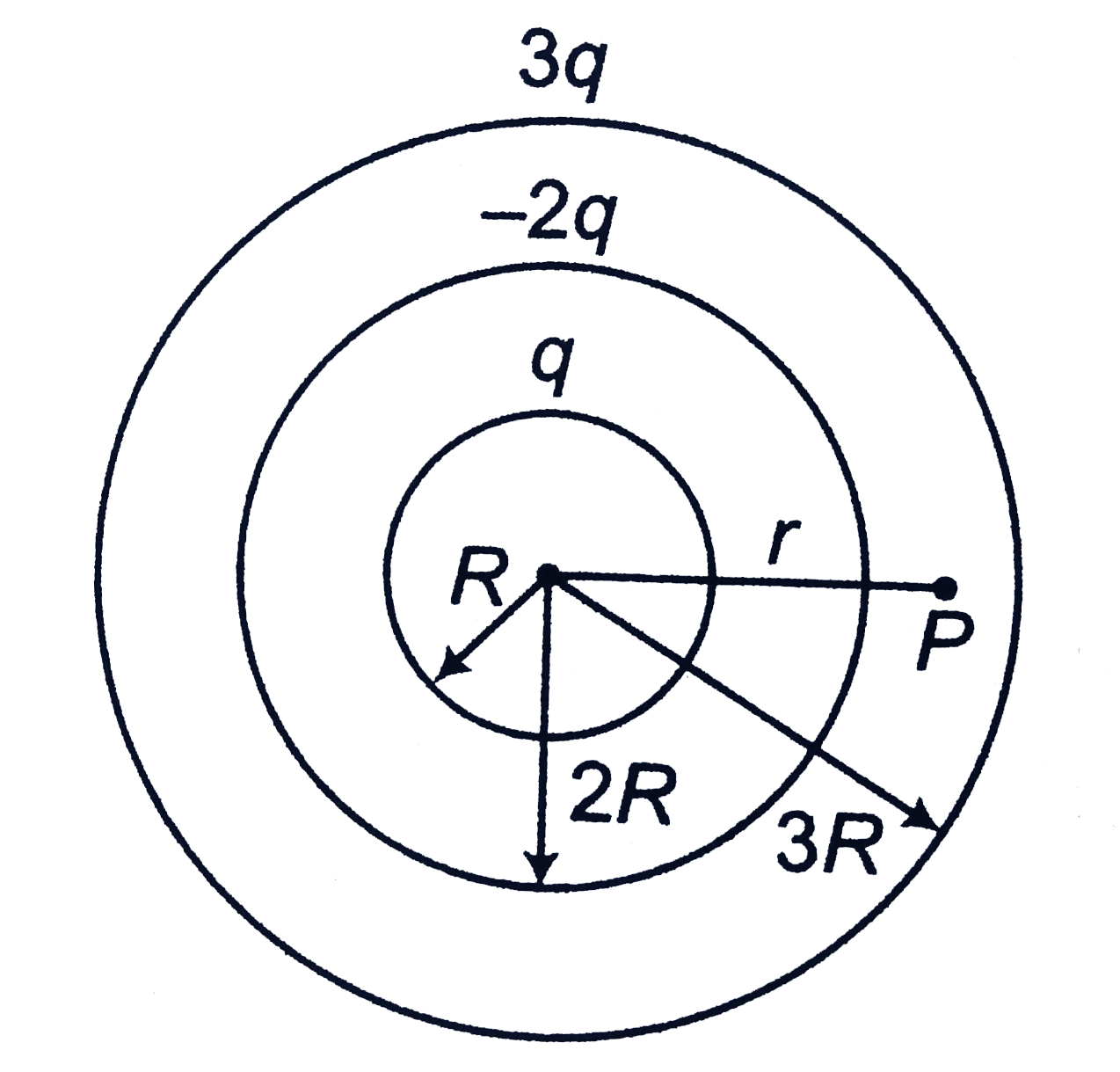
View SolutionThree conducting spherical shells have charges q,−2q and 3q as shown in figure. Find electric Potential at point P as shown in figure.
View Solution3 charges are placed in a circle of radius d as shown in figure. Find the electric field along x-axis at centre of circle.

View Solution3 charges are placed in a circle of radius d as shown in figure. Find the electric field along x-axis at centre of circle.

View SolutionA tiny electric dipole of dipole moment →P=P0ˆj is placed at point (l,0). There exists an electric field →E=2ax2ˆi+(2by2+2cy)ˆj.
View SolutionAn electric dipole of moment rp=(ˆi+2ˆj)×10−28Cm is at origin. The electric field at point ( 2,4) due to the dipole is parallelto
View SolutionAn electric dipole of moment rp=(ˆi+2ˆj)×10−28Cm is at origin. The electric field at point ( 2,4) due to the dipole is parallelto
View Solution
