A parallel plate capacitor consist of two circular plates of area 0.04m2 each. They are separated by a distance 0.4 mm. If displacement current between the plates is 6A then rate of change in electric field between the plate w.r.t. time will be
1.7x1010Vm−1's−1
1.7x1013Vm−1's−1
3.7x1011Vm−1's−1
4.7x1012Vm's−1Vm−1's−1
To solve the problem, we need to find the rate of change of the electric field (dE/dt) between the plates of a parallel plate capacitor, given the displacement current (Id), the area of the plates (A), and the permittivity of free space (ε0).
1. Identify the given values:
- Area of the plates, A=0.04m2
- Distance between the plates, d=0.4mm=0.4×10−3m
- Displacement current, Id=6A
- Permittivity of free space, ϵ0=8.85×10−12F/m
2. Use the formula for displacement current:
The displacement current Id is related to the rate of change of electric field dE/dt by the formula:
Id=ϵ0⋅A⋅dEdt
3. Rearrange the formula to solve for dE/dt:
dEdt=Idϵ0⋅A
4. Substitute the known values into the equation:
dEdt=6A(8.85×10−12F/m)⋅(0.04m2)
5. Calculate the denominator:
ϵ0⋅A=8.85×10−12⋅0.04=3.54×10−13F
6. Calculate dE/dt:
dEdt=63.54×10−13≈1.69×1013V/m/s
7. Round the answer:
dEdt≈1.7×1013V/m/s
Final Answer:
dEdt≈1.7×1013V/m/s
- Area of the plates, A=0.04m2
- Distance between the plates, d=0.4mm=0.4×10−3m
- Displacement current, Id=6A
- Permittivity of free space, ϵ0=8.85×10−12F/m
The displacement current Id is related to the rate of change of electric field dE/dt by the formula:
Id=ϵ0⋅A⋅dEdt
dEdt=Idϵ0⋅A
dEdt=6A(8.85×10−12F/m)⋅(0.04m2)
ϵ0⋅A=8.85×10−12⋅0.04=3.54×10−13F
dEdt=63.54×10−13≈1.69×1013V/m/s
dEdt≈1.7×1013V/m/s
dEdt≈1.7×1013V/m/s
Similar Questions
A parallel plate capacitor consists of two circular plates of radius R=0.1 m. they are separated by a distance d=0.5mm, if electric field between the capacitor plates changes as dEdt=5×1013Vm×s. Find displacement current between the plates.
View SolutionA parallel plate capacitor consists of two circular plates of radius 0.05 m. If electric field between the plate is change as dEdt=1010Vm−s, then find displacement current between the plates.
View SolutionA parallel plate capacitor consists of two circular plates each of radius 2cm, separated by a distance of 0.1mm. If the potential difference across the plates is varying at the rate of 5×106Vs−1, then the value of displacement current is
View SolutionA parallel plate capacitor consists of two circular plate of radius R=0.1m. They are separated by a short distance. If electric field between the capacitor plates changes as dEdt=6×1013Vm×s. Find displacement current between the plates.
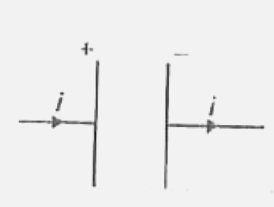
View SolutionA parallel plate capacitor with circular plates of radius R is being charged as shown. At the instant shown, the displacement current in the region between the plates enclosed between R2 and R is given by
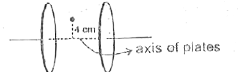
View SolutionTwo circular plates of radius 0.1 m are used to form a parallel capacitor. If displacement current between the plates is 2π ampere, then find magnetic produced by displacement current 4 cm from the axis of the plates.
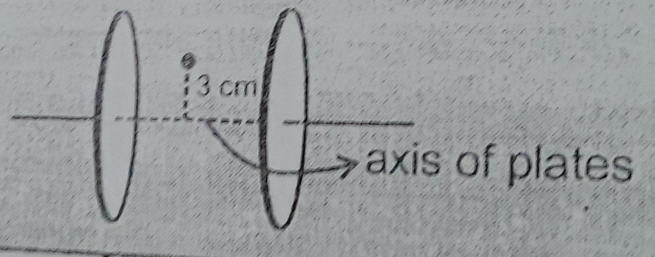
View SolutionTwo circular plates of radius 0.1m are used to from a parallel plate capacitor. If displacement current between the plates is 2π.ampere, then find m agnetic filed produced by displacement current 4 cm from the axis of the plates.
View SolutionA parallel plate capacitor is made of two circular plates separated by a distance 5mm and with a dielectric of dielectric constant 2.2 between them. When the electric field in the dielectric is 3×104V/m the charge density of the positive plate will be close to:
View SolutionA parallel plate capicitaor with plates of area 1m2 each, are at a separation of 0.1m. If the electric field between the plates is 100 N/C, the magnitude of charge on each plate is : (Take ε=8.85×10−12C2N−m2)
View SolutionTwo parallel metal plates having charges +Q and −Q face each other at a certain distance between them.If the plates are now dipped in kerosene oil tank ,the electric field between the plates will
View Solution
