A parallel plate capacitor consists of two circular plate of radius R=0.1m. They are separated by a short distance. If electric field between the capacitor plates changes as dEdt=6×1013Vm×s. Find displacement current between the plates.
To find the displacement current between the plates of a parallel plate capacitor, we can follow these steps:
Step 1: Understand the formula for displacement current
The displacement current Id can be calculated using the formula:
Id=ϵ0dΦdt
where ϵ0 is the permittivity of free space and Φ is the electric flux.
Step 2: Relate electric flux to electric field
The electric flux Φ can be expressed as:
Φ=E⋅A
where E is the electric field and A is the area of the plates.
Step 3: Substitute the expression for flux into the displacement current formula
Substituting Φ into the displacement current formula gives:
Id=ϵ0ddt(E⋅A)
Since the area A is constant, we can take it outside the derivative:
Id=ϵ0AdEdt
Step 4: Calculate the area of the circular plates
The area A of a circular plate is given by:
A=πR2
Substituting R=0.1m:
A=π(0.1)2=π⋅0.01≈0.0314m2
Step 5: Substitute the known values into the displacement current formula
Now, substituting ϵ0=8.85×10−12F/m, A≈0.0314m2, and dEdt=6×1013V/(m⋅s):
Id=(8.85×10−12)⋅(0.0314)⋅(6×1013)
Step 6: Perform the calculation
Calculating the above expression:
Id=8.85×10−12⋅0.0314⋅6×1013
Calculating 8.85×0.0314:
8.85×0.0314≈0.277
Now, multiplying by 6×1013:
Id≈0.277×6×1013≈1.662×1013A
Step 7: Final result
Thus, the displacement current Id is approximately:
Id≈16.67A
The displacement current Id can be calculated using the formula:
Id=ϵ0dΦdt
where ϵ0 is the permittivity of free space and Φ is the electric flux.
The electric flux Φ can be expressed as:
Φ=E⋅A
where E is the electric field and A is the area of the plates.
Substituting Φ into the displacement current formula gives:
Id=ϵ0ddt(E⋅A)
Since the area A is constant, we can take it outside the derivative:
Id=ϵ0AdEdt
The area A of a circular plate is given by:
A=πR2
Substituting R=0.1m:
A=π(0.1)2=π⋅0.01≈0.0314m2
Now, substituting ϵ0=8.85×10−12F/m, A≈0.0314m2, and dEdt=6×1013V/(m⋅s):
Id=(8.85×10−12)⋅(0.0314)⋅(6×1013)
Calculating the above expression:
Id=8.85×10−12⋅0.0314⋅6×1013
Calculating 8.85×0.0314:
8.85×0.0314≈0.277
Now, multiplying by 6×1013:
Id≈0.277×6×1013≈1.662×1013A
Thus, the displacement current Id is approximately:
Id≈16.67A
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Check point 8.110videos
ELECTROMAGNETIC WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Check point 8.215videos
ELECTROMAGNETIC WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise Subjective11videos
ELECTROMAGNETIC WAVES
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises50videos
ELECTROSTATIC POTENTIAL AND CAPACITORS
Similar Questions
A parallel plate capacitor consists of two circular plates of radius R=0.1 m. they are separated by a distance d=0.5mm, if electric field between the capacitor plates changes as dEdt=5×1013Vm×s. Find displacement current between the plates.
View SolutionA parallel plate capacitor consists of two circular plates of radius 0.05 m. If electric field between the plate is change as dEdt=1010Vm−s, then find displacement current between the plates.
View SolutionA parallel plate capacitor consists of two circular plates each of radius 2cm, separated by a distance of 0.1mm. If the potential difference across the plates is varying at the rate of 5×106Vs−1, then the value of displacement current is
View SolutionA parallel plate capacitor consist of two circular plates of area 0.04m2 each. They are separated by a distance 0.4 mm. If displacement current between the plates is 6A then rate of change in electric field between the plate w.r.t. time will be
View SolutionA parallel plate capacitor has circular plates each of radius 5.0 cm. It is being charged so that electric field in the gap between its plates rises steadily at the rate of 2×1012Vm−1s−1What is the displacement current.
View SolutionA parallel plate capacitor has circular plates, each of radius 5.0cm. It is being charged so that electric field in the gap between its plates rises steadily at the rate of 1012Vm−1s−1.What is the displacement current?
View SolutionA parallel plate capacitor with circular plates of radius R is being charged as shown. At the instant shown, the displacement current in the region between the plates enclosed between R2 and R is given by
 View Solution
View SolutionIf potential difference between the plates of capacitor changes with rate of dVdt=106voltsec, and capacitance of capacitors is 1μF, then find displacement current between the plates.
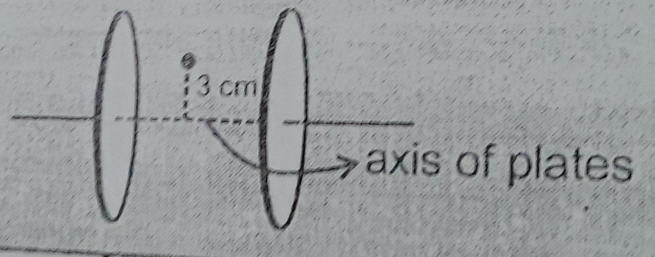
View SolutionTwo circular plates of radius 0.1m are used to from a parallel plate capacitor. If displacement current between the plates is 2π.ampere, then find m agnetic filed produced by displacement current 4 cm from the axis of the plates.
 View Solution
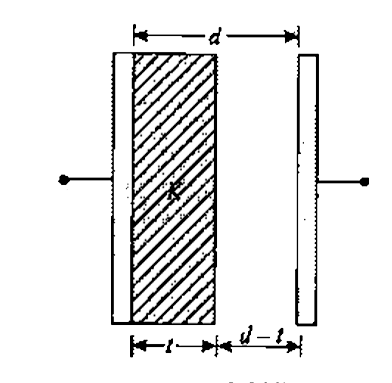
View SolutionA parallel plate capacitor consists of two metal plates of area A and separation d. A slab of thickness t and electric constant K is inserted between the plates with its faces parallel to the plates and having the same surface area as that of the plates. Find the capacitance of the system.
IF K=2, for what value of t/d will the capacitance of the system be 3/2 times that of the air capacitor? Calculate the energy in the two cases and account for the energy change.
 View Solution
View Solution

