A particle of mass 'm' is moving on a circular path of radius 'r' with uniform speed 'v'. Rate of change of linear momentum is
A. Proportional to radius 'r'
B. Proportional to v2
C. Zero
D. Independent of speed
The correct Answer is:B
To find the rate of change of linear momentum for a particle of mass 'm' moving in a circular path of radius 'r' with uniform speed 'v', we can follow these steps:
1. Understanding Linear Momentum:
The linear momentum (P) of an object is given by the product of its mass (m) and its velocity (v):
P=m⋅v
2. Identifying the Nature of Motion:
Since the particle is moving in a circular path with uniform speed, even though the speed is constant, the direction of the velocity is continuously changing. This means there is an acceleration acting on the particle, known as centripetal acceleration.
3. Centripetal Force and Acceleration:
The centripetal acceleration (a) for an object moving in a circle of radius 'r' at speed 'v' is given by:
a=v2r
The force required to maintain this circular motion (centripetal force, F) is:
F=m⋅a=m⋅v2r
4. Rate of Change of Linear Momentum:
The rate of change of linear momentum (which is also the net force acting on the object) can be expressed as:
dPdt=F
Substituting the expression for centripetal force, we have:
dPdt=m⋅v2r
5. Final Expression:
Therefore, the rate of change of linear momentum is:
dPdt=mv2r
Conclusion:
The rate of change of linear momentum for a particle of mass 'm' moving in a circular path of radius 'r' with uniform speed 'v' is given by:
dPdt=mv2r
The linear momentum (P) of an object is given by the product of its mass (m) and its velocity (v):
P=m⋅v
Since the particle is moving in a circular path with uniform speed, even though the speed is constant, the direction of the velocity is continuously changing. This means there is an acceleration acting on the particle, known as centripetal acceleration.
The centripetal acceleration (a) for an object moving in a circle of radius 'r' at speed 'v' is given by:
a=v2r
The force required to maintain this circular motion (centripetal force, F) is:
F=m⋅a=m⋅v2r
The rate of change of linear momentum (which is also the net force acting on the object) can be expressed as:
dPdt=F
Substituting the expression for centripetal force, we have:
dPdt=m⋅v2r
Therefore, the rate of change of linear momentum is:
dPdt=mv2r
The rate of change of linear momentum for a particle of mass 'm' moving in a circular path of radius 'r' with uniform speed 'v' is given by:
dPdt=mv2r
Topper's Solved these Questions
Similar Questions
A particle is moving on a circular path of radius 10m with uniform speed of 4ms−1.The magnitude of change in velocity of particle when it completes a semi circular path is
View Solution
A particle is moving on a circular path of radius r with uniform velocity v. The change in velocity when the particle moves from P to Q is (∠POQ=40∘)
View Solution
Knowledge Check
A particle is moving on a circular path of radius r with uniform speed v. What is the displacement of the particle after it has described an angle of 60∘?
Ar√2Br√3CrD2r
The acceleration of an object moving in a circle of radius R with uniform speed v is
View SolutionA particle of-mass m moves along a circular path of radius r with velocity v. What is its instantaneous angular momentum about a point on the plane of the orbit at a distance x from the centre of the axis of rotation.
View SolutionA particle of mass m, moving in a circular path of radius R with a constant speed v2 is located at point (2R, 0) at time t = 0 and a man starts moving with a velocity v0 along the positive y-axis from origin at time t = 0. Calculate the linear momentum of the particle w.r.t. man as a function of time ______________.

View SolutionA Particle of mass 'M' moves in a uniform circular path of radius 'r' with a constant speed 'v' then its centripetal acceleration is .
View SolutionA paticle of mass m is executing uniform circular motion on a path of radius r. If p is the magnitude of its linear momentum, then the radial force acting on the particle is
View SolutionA particle of charge 'q' and mass 'm' move in a circular orbit of radius 'r' with frequency 'v' the ratio of the magnetic moment to angular momentum is:
View SolutionA particle of mass m is moving in a circle of radius (r) with changing speed (v) the direction of centripetal force and tangential force are shown below the value of α is
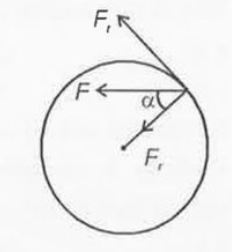
View Solution