Two blocks A and B having masses 5 kg and 10 kg respectively connected through a massless string which is passing over a pulley (disc) of mass 2 kg and radius 25 cm as shown in figure If system is. released from rest. then angular acceleration of the pulley is (String does not slip over the pulley horizontal surface is smooth and
The correct Answer is:C
To find the angular acceleration of the pulley in the given system, we can follow these steps:
Step 1: Identify the forces acting on the blocks
- For block A (mass = 5 kg), the forces are:
- Weight (downward): WA=mA⋅g=5⋅10=50N
- Tension in the string (upward): TA
- For block B (mass = 10 kg), the forces are:
- Weight (downward): WB=mB⋅g=10⋅10=100N
- Tension in the string (upward): TB
Step 2: Write the equations of motion for both blocks
- For block A (moving upwards):
TA=mA⋅g−mA⋅a(1)
Substituting mA=5kg:
TA=50−5a
- For block B (moving downwards):
mB⋅g−TB=mB⋅a(2)
Substituting mB=10kg:
100−TB=10a
Step 3: Relate the tensions to the pulley
The net torque (τ) on the pulley can be expressed in terms of the tensions:
τ=(TB−TA)⋅r
Where r=0.25m (25 cm converted to meters).
The moment of inertia (I) of the pulley (disc) is given by:
I=12mpulleyr2=12⋅2⋅(0.25)2=12⋅2⋅0.0625=0.0625kg m2
The angular acceleration (α) is related to the linear acceleration (a) by:
α=ar
Step 4: Write the equation for torque
Using τ=I⋅α:
(TB−TA)⋅0.25=0.0625⋅α
Substituting α=a0.25:
(TB−TA)⋅0.25=0.0625⋅a0.25
Simplifying gives:
(TB−TA)=0.25⋅0.25⋅a=0.015625a(3)
Step 5: Substitute equations (1) and (2) into (3)
Substituting TA and TB from equations (1) and (2) into equation (3):
(100−10a)−(50−5a)=0.015625a
Simplifying:
100−10a−50+5a=0.015625a
50−5a=0.015625a
Combining like terms:
50=5a+0.015625a
50=5.015625a
a=505.015625≈9.95m/s2
Step 6: Calculate angular acceleration
Now, substituting a back to find α:
α=ar=9.950.25≈39.8rad/s2
Final Answer
The angular acceleration of the pulley is approximately 39.8rad/s2.
---
- For block A (mass = 5 kg), the forces are:
- Weight (downward): WA=mA⋅g=5⋅10=50N
- Tension in the string (upward): TA
- Weight (downward): WB=mB⋅g=10⋅10=100N
- Tension in the string (upward): TB
- For block A (moving upwards):
TA=mA⋅g−mA⋅a(1)
Substituting mA=5kg:
TA=50−5a
mB⋅g−TB=mB⋅a(2)
Substituting mB=10kg:
100−TB=10a
The net torque (τ) on the pulley can be expressed in terms of the tensions:
τ=(TB−TA)⋅r
Where r=0.25m (25 cm converted to meters).
I=12mpulleyr2=12⋅2⋅(0.25)2=12⋅2⋅0.0625=0.0625kg m2
α=ar
Using τ=I⋅α:
(TB−TA)⋅0.25=0.0625⋅α
Substituting α=a0.25:
(TB−TA)⋅0.25=0.0625⋅a0.25
Simplifying gives:
(TB−TA)=0.25⋅0.25⋅a=0.015625a(3)
Substituting TA and TB from equations (1) and (2) into equation (3):
(100−10a)−(50−5a)=0.015625a
Simplifying:
100−10a−50+5a=0.015625a
50−5a=0.015625a
Combining like terms:
50=5a+0.015625a
50=5.015625a
a=505.015625≈9.95m/s2
Now, substituting a back to find α:
α=ar=9.950.25≈39.8rad/s2
The angular acceleration of the pulley is approximately 39.8rad/s2.
Similar Questions
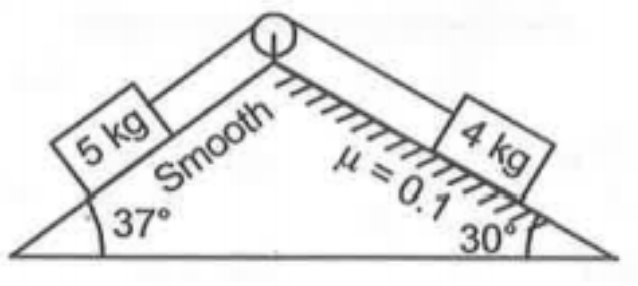
Two blocks of masses 5 kg and 4 kg are connected with ideal string which is passing over an ideal pulley as shown in figure. If the system is released from rest then the magnitude of acceleration of the blocks will be (Take g=10ms−2and√3=1.7)
View SolutionTwo blocks of masses 10 kg and 9 kg are connected with light string which is passing over an ideal pulley as shown in figure. If system is released from rest then the acceleration of 9 kg block at the given instant is about (Assume all the surfaces are smooth and g=10ms2)
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two blocks each of mass 4 kg connected by a light string which is passing over an ideal pulley is as shown in figure. If the system is released from rest then the acceleration (in m/s2) of centre of mass is (g = 10 m/s2)
View SolutionThree blocks A, B and C of masses 5 kg, 5 kg and 10 kg respectively are connected with two light strings, one of them is passing over an ideal pulley The system is released from rest on smooth inclined plane of inclination 30" as shown in figure. The value of tension T1T2 is
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo masses of 10 kg and 20 kg are connected with an inextensible string passing over two smooth pulleys as shown in the figure. The acceleration of 20 kg mass will be :
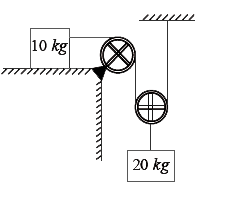
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionTwo unequal masses of 1 kg and 2 kg are attached at the two ends of a light inextensible string passing over a smooth pulley as shown in figure. If the system is released from rest, find the work done by string on both the blocks in 1 s. (Take g = 10 ms−2)

View SolutionTwo unequal masses of 1kg and 2kg are connected by a string going over a clamed light smooth pulley as shown in figure . The system is released from rest .The larger mass is stopped for a moment 1.0s after the system is set in motion.Find the time elapsed before the string is tight again.

View Solution
