Three blocks A, B and C of masses 5 kg, 5 kg and 10 kg respectively are connected with two light strings, one of them is passing over an ideal pulley The system is released from rest on smooth inclined plane of inclination 30" as shown in figure. The value of tension T1T2 is
12
2
√32
2√3
The correct Answer is:B
To find the ratio of tensions T1T2 in the given system of blocks, we will analyze the forces acting on each block and apply Newton's second law.
1. Identify the Forces on Each Block:
- Block A (mass = 5 kg) and Block B (mass = 5 kg) are on the inclined plane.
- Block C (mass = 10 kg) is hanging vertically.
- The angle of inclination θ=30∘.
2. Calculate the Gravitational Force Components:
- For Block A and Block B, the gravitational force acting down the incline is given by:
Fgravity, incline=m⋅g⋅sin(θ)
- For both Block A and Block B:
Fgravity, incline=5⋅9.8⋅sin(30∘)=5⋅9.8⋅0.5=24.5N
3. Set Up the Equations of Motion:
- For Block A:
T2−mA⋅g⋅sin(30∘)=mA⋅a
T2−24.5=5a(1)
- For Block B (similar to Block A):
T2−mB⋅g⋅sin(30∘)=mB⋅a
T2−24.5=5a(2)
- For Block C:
T1−mC⋅g=−mC⋅a
T1−10⋅9.8=−10a
T1=98−10a(3)
4. Equate the Tension Equations:
- From equations (1) and (2), we see that both give the same expression for T2:
T2=24.5+5a
- Substitute T2 into equation (3):
T1=98−10a
5. Find the Acceleration a:
- Since the system is connected, we can express the net force:
T1−2T2=0(since both A and B are pulling against C)
- Substitute T1 and T2:
(98−10a)−2(24.5+5a)=0
98−10a−49−10a=0
49=20a
a=4920=2.45m/s2
6. Calculate T1 and T2:
- Substitute a back into T2:
T2=24.5+5(2.45)=24.5+12.25=36.75N
- Substitute a back into T1:
T1=98−10(2.45)=98−24.5=73.5N
7. Find the Ratio T1T2:
T1T2=73.536.75=2
Final Answer:
The value of T1T2 is 2.
---
- Block A (mass = 5 kg) and Block B (mass = 5 kg) are on the inclined plane.
- Block C (mass = 10 kg) is hanging vertically.
- The angle of inclination θ=30∘.
- For Block A and Block B, the gravitational force acting down the incline is given by:
Fgravity, incline=m⋅g⋅sin(θ)
- For both Block A and Block B:
Fgravity, incline=5⋅9.8⋅sin(30∘)=5⋅9.8⋅0.5=24.5N
- For Block A:
T2−mA⋅g⋅sin(30∘)=mA⋅a
T2−24.5=5a(1)
T2−mB⋅g⋅sin(30∘)=mB⋅a
T2−24.5=5a(2)
T1−mC⋅g=−mC⋅a
T1−10⋅9.8=−10a
T1=98−10a(3)
- From equations (1) and (2), we see that both give the same expression for T2:
T2=24.5+5a
- Substitute T2 into equation (3):
T1=98−10a
- Since the system is connected, we can express the net force:
T1−2T2=0(since both A and B are pulling against C)
- Substitute T1 and T2:
(98−10a)−2(24.5+5a)=0
98−10a−49−10a=0
49=20a
a=4920=2.45m/s2
- Substitute a back into T2:
T2=24.5+5(2.45)=24.5+12.25=36.75N
- Substitute a back into T1:
T1=98−10(2.45)=98−24.5=73.5N
T1T2=73.536.75=2
The value of T1T2 is 2.
Similar Questions
Two block of masses 2kg and 4kg are released from rest over a smooth inclined place of inclination 30∘ as shown in figure what is the normal force between the two blocks?

View SolutionTwo blocks of masses 10 kg and 9 kg are connected with light string which is passing over an ideal pulley as shown in figure. If system is released from rest then the acceleration of 9 kg block at the given instant is about (Assume all the surfaces are smooth and g=10ms2)
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
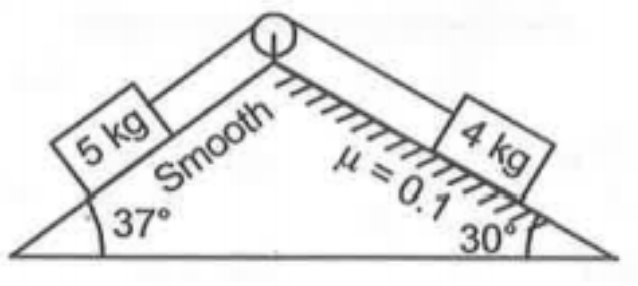
Two blocks of masses 5 kg and 4 kg are connected with ideal string which is passing over an ideal pulley as shown in figure. If the system is released from rest then the magnitude of acceleration of the blocks will be (Take g=10ms−2and√3=1.7)
View SolutionTwo bodies of masses 1 kg and 2 kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string
View SolutionTwo blocks each of mass 4 kg connected by a light string which is passing over an ideal pulley is as shown in figure. If the system is released from rest then the acceleration (in m/s2) of centre of mass is (g = 10 m/s2)
View Solution
Three blocks A, B and C havig masses m kg, 2kg and 3 kg are attached by massless strings and ideal pulleys as shown in the figure. When the system is realeased from rest if the block A remains stationary. the mass of block A is
View SolutionThree blocks, P, Q and R of masses 5 kg, 4 kg and 3 kg respectively are connected by a light inextensible string and they are moved on a smooth horizontal plane. If a force of 24 N is applied to the string connected to R, tensions T1andT2 in the string are

View SolutionTwo blocks A and B having masses 5 kg and 10 kg respectively connected through a massless string which is passing over a pulley (disc) of mass 2 kg and radius 25 cm as shown in figure If system is. released from rest. then angular acceleration of the pulley is (String does not slip over the pulley horizontal surface is smooth and g=10ms−2 (∀KTST02_N∃TPHYE02011_Q01)
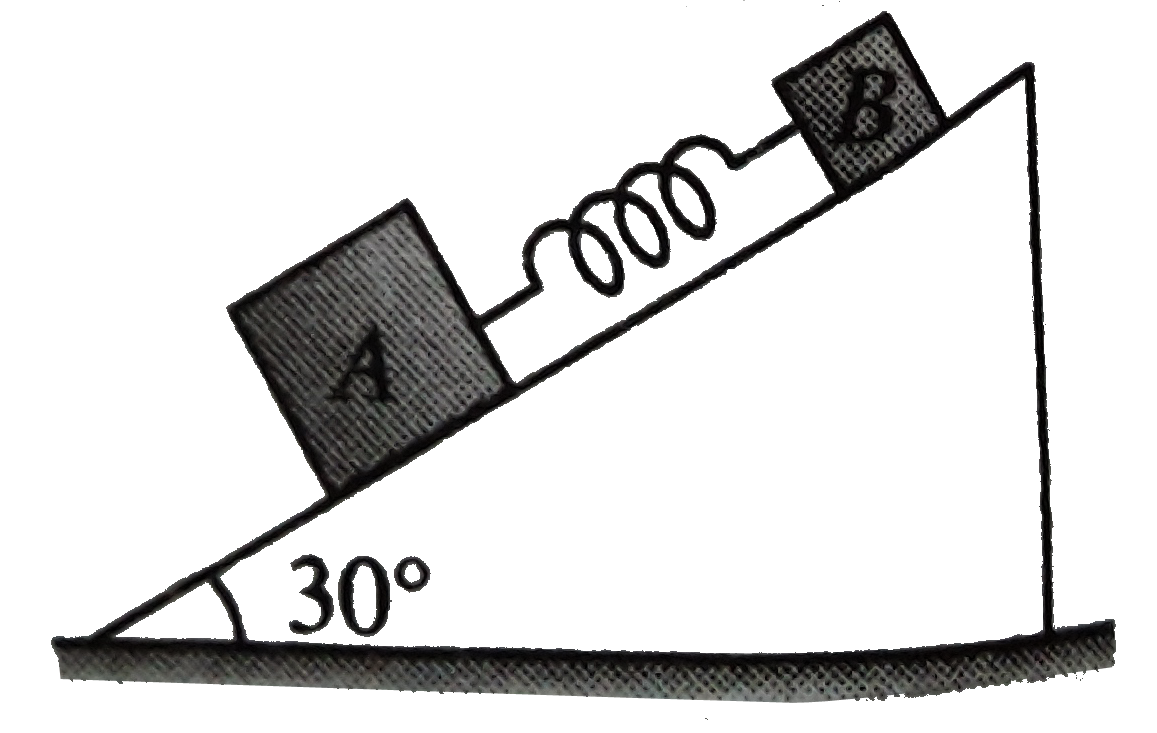
View SolutionTwo blocks A and B of masses 5kg and 2kg respectively connected by a spring of force constant =100Nm−1 are placed on an inclined plane of inclined 30∘ as shown in figure If the system is released from rest
View Solution
