The ratio of the density and pressure of a fixed mass of an ideal gas is "5" at 10°C. Then this ratio at 110°C is
3.69
5
8.46
6.76
The correct Answer is:A
To solve the problem, we need to find the ratio of density to pressure of a fixed mass of an ideal gas at two different temperatures. We know that the ratio of density (ρ) to pressure (P) at 10°C is 5, and we want to find this ratio at 110°C.
1. Convert Temperatures to Kelvin:
- The temperature at 10°C in Kelvin is:
T1=10+273=283K
- The temperature at 110°C in Kelvin is:
T2=110+273=383K
2. Use the Ideal Gas Law:
- The ideal gas law states that:
PV=nRT
- Rearranging this gives us:
P=mV⋅RM⋅T
- Here, mV is the density (ρ), so we can express pressure as:
P=ρ⋅RM⋅T
3. Find the Ratio of Density to Pressure:
- From the rearrangement, we can express the ratio of density to pressure as:
ρP=MR⋅T
- This shows that the ratio ρP is inversely proportional to the temperature (T).
4. Set Up the Ratios:
- We can set up the ratio of the densities and pressures at the two temperatures:
ρ2P2=MR⋅T2
- And we know:
ρ1P1=MR⋅T1
- Therefore, we can write:
ρ2P2=T1T2⋅ρ1P1
5. Substituting Known Values:
- We know that ρ1P1=5 (given in the problem).
- Substituting the values:
ρ2P2=283383⋅5
6. Calculate the Final Value:
- Performing the calculation:
ρ2P2=283×5383=1415383≈3.69
Conclusion:
The ratio of density to pressure at 110°C is approximately 3.69.
- The temperature at 10°C in Kelvin is:
T1=10+273=283K
- The temperature at 110°C in Kelvin is:
T2=110+273=383K
- The ideal gas law states that:
PV=nRT
- Rearranging this gives us:
P=mV⋅RM⋅T
- Here, mV is the density (ρ), so we can express pressure as:
P=ρ⋅RM⋅T
- From the rearrangement, we can express the ratio of density to pressure as:
ρP=MR⋅T
- This shows that the ratio ρP is inversely proportional to the temperature (T).
- We can set up the ratio of the densities and pressures at the two temperatures:
ρ2P2=MR⋅T2
- And we know:
ρ1P1=MR⋅T1
- Therefore, we can write:
ρ2P2=T1T2⋅ρ1P1
- We know that ρ1P1=5 (given in the problem).
- Substituting the values:
ρ2P2=283383⋅5
- Performing the calculation:
ρ2P2=283×5383=1415383≈3.69
The ratio of density to pressure at 110°C is approximately 3.69.
Topper's Solved these Questions
Similar Questions
At 10∘C, the value of the density of a fixed mass of an ideal gas divided by its pressure is x. at 110∘C, this ratio is
View SolutionThe following graphs shows two isothermal process for a fixed mass of an ideal gas. Find the ratio of r.m.s speed of the molecules at temperatures T1 and T2?
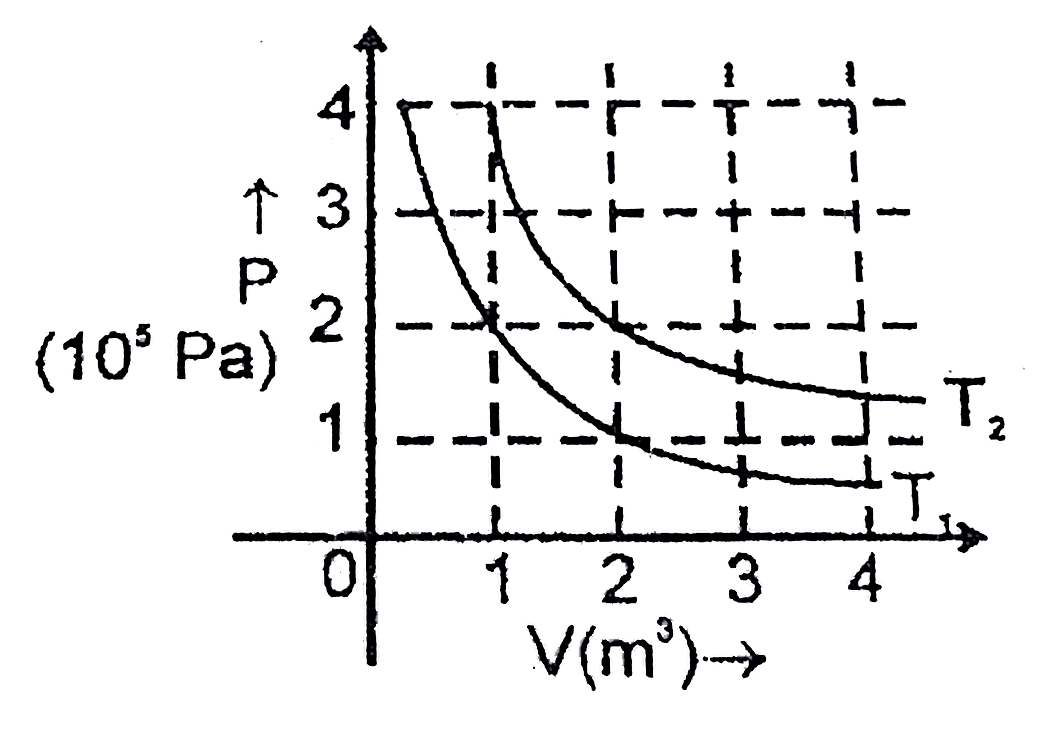
View SolutionThe molar specific heat at constant pressure of an ideal gas is (7/2R). The ratio of specific heat at constant pressure to that at constant volume is
View SolutionIf E is the energy density in an ideal gas, then the pressure of the ideal gas is
View SolutionFigure shows the isotherms of a fixed mass of an ideal gas at three temperatures TA,TB and TC , then

View SolutionThe following graphs shows two isotherms for a fixed mass of an ideal gas. Find the ratio of r.m.s speed of the molecules at tempertaures T1 and T2?
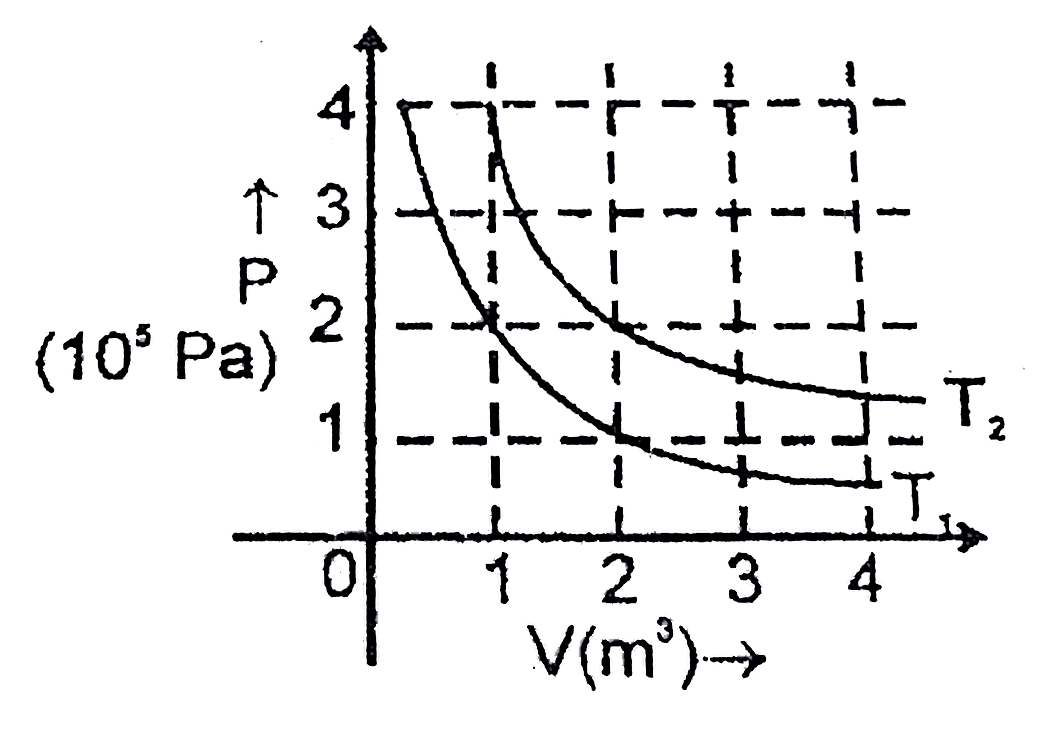
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and a final pressure Pi, If the same gas is expanded adiabatically to a volume 2V, the final pressure Pa. The ratio of the specific heats of the gas is 1.67. The ratio PaP1 is .......
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and a final pressure Pi, If the same gas is expanded adiabatically to a volume 2V, the final pressure Pa. The ratio of the specific heats of the gas is 1.67. The ratio PaP1 is .......
View SolutionThe ratio of the molar heat capacities of an ideal gas is (CpCv=76). Calculate the change in internal energy of 1.0mole of the gas when its temperature is raised by 50K, (a) keeping the pressure constant , (b) keeping the volume constant and (c ) adiabatically.
View SolutionAt STP the density of a gas X is three times that of gas Y while molecule mass of gas Y is twice that of X. The ratio of pressures of X and Y will be:
View Solution