A block of mass m1 resting on a frictionless horizontal surface is connected to a spring of spring constant k that is anchored in a near by wall. A block of mass m2 is placed on the top of the first block. The coefficient of static friction between the two blocks is μ Assuming that the two blocks move together as a unit, find the period of oscillation of the system and also find maximum oscillation amplitude that permits the two bodies to move as a unit.
2π√m1+m2k,(mum_2g)/k
2π√m1+m2k, (μm1g)/k
2π√m1+m2k,(μ(m1+m2))/k
2π√m1+m2k, (μg(m1+m2))/k
To solve the problem step by step, we will break it down into two parts: finding the period of oscillation of the system and finding the maximum oscillation amplitude that permits the two bodies to move as a unit.
Step 1: Find the Period of Oscillation
1. Identify the total mass of the system:
The total mass m of the system is the sum of the masses of the two blocks:
m=m1+m2
2. Use the formula for the period of a mass-spring system:
The formula for the period T of oscillation for a mass-spring system is given by:
T=2π√mk
3. Substitute the total mass into the formula:
Substitute m=m1+m2 into the period formula:
T=2π√m1+m2k
Step 2: Find the Maximum Oscillation Amplitude
1. Determine the angular frequency:
The angular frequency ω of the system is given by:
ω=√km1+m2
2. Calculate the maximum force on the upper block:
The maximum force Fmax acting on the upper block (mass m2) due to the acceleration is:
Fmax=m2⋅amax=m2⋅(Amax⋅ω2)
where Amax is the maximum amplitude.
3. Frictional force:
The maximum static frictional force Ffriction that can act between the two blocks is:
Ffriction=μ⋅m2⋅g
4. Set the maximum force equal to the frictional force:
For the upper block not to slip, the maximum force must not exceed the maximum static frictional force:
m2⋅(Amax⋅ω2)≤μ⋅m2⋅g
5. Cancel m2 from both sides (assuming m2≠0):
Amax⋅ω2≤μ⋅g
6. Substitute ω2:
Substitute ω2=km1+m2 into the inequality:
Amax⋅km1+m2≤μ⋅g
7. Solve for Amax:
Rearranging gives:
Amax≤μ⋅g⋅(m1+m2)k
Final Answers:
- The period of oscillation T is:
T=2π√m1+m2k
- The maximum oscillation amplitude Amax that permits the two bodies to move as a unit is:
Amax=μ⋅g⋅(m1+m2)k
The total mass m of the system is the sum of the masses of the two blocks:
m=m1+m2
The formula for the period T of oscillation for a mass-spring system is given by:
T=2π√mk
Substitute m=m1+m2 into the period formula:
T=2π√m1+m2k
The angular frequency ω of the system is given by:
ω=√km1+m2
The maximum force Fmax acting on the upper block (mass m2) due to the acceleration is:
Fmax=m2⋅amax=m2⋅(Amax⋅ω2)
where Amax is the maximum amplitude.
The maximum static frictional force Ffriction that can act between the two blocks is:
Ffriction=μ⋅m2⋅g
For the upper block not to slip, the maximum force must not exceed the maximum static frictional force:
m2⋅(Amax⋅ω2)≤μ⋅m2⋅g
Amax⋅ω2≤μ⋅g
Substitute ω2=km1+m2 into the inequality:
Amax⋅km1+m2≤μ⋅g
Rearranging gives:
Amax≤μ⋅g⋅(m1+m2)k
- The period of oscillation T is:
T=2π√m1+m2k
- The maximum oscillation amplitude Amax that permits the two bodies to move as a unit is:
Amax=μ⋅g⋅(m1+m2)k
Topper's Solved these Questions
Similar Questions
A block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View SolutionThe block of mass M and are arrenged as the situation in fig is shown.The coefficient of friction between two block is μand that between the bigger block and the ground is μ find the acceleration of the block .
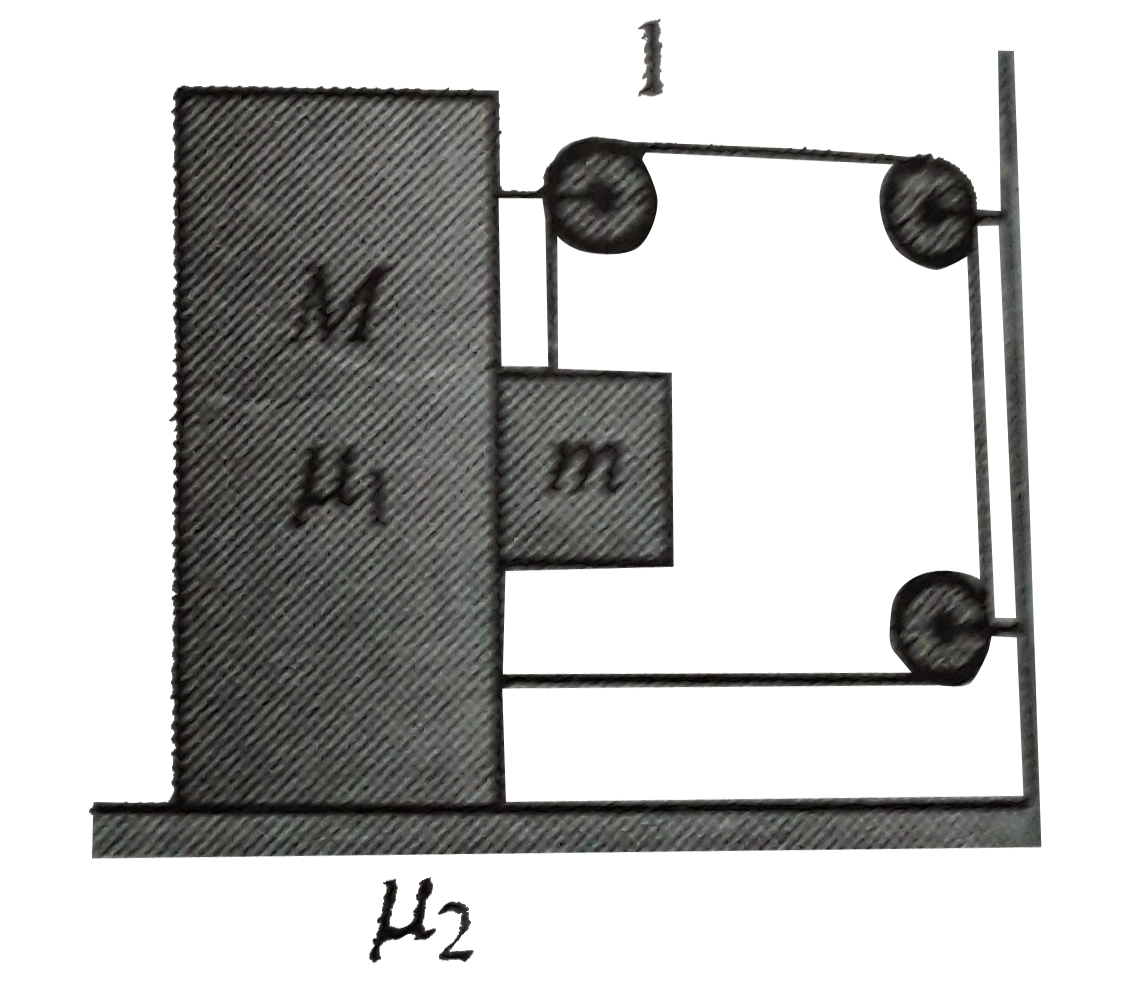
View Solution
Knowledge Check
A block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
A10NB5NC2.5ND20N
A block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA block of mass m is moving on a rough horizontal surface. μ is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
View SolutionA block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
View SolutionA block of mass M is being pulley along horizontal surface .The coefficient of friction the block and the surface is μ If another block of mass M/2 is placed on the block and it is pulled is again pulled on the surface , the coefficient of friction the block and the surface will be
View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View SolutionA block of massm is placed on another block of mass M which itself is lying on a horizontal surface .The coefficient of friction between two blocks is μ1and that between the block of mass M and horizontal surfece is μ2 What maximum horizontal force can be applied to the lower block move without separation?

View Solution
