A body moves along a straight line OAB simple harmonically. It has zero velocity at the points A and B which are at distances 'a' and b'respectivelyom0' and has velocity 'V' when halfway between them then the period of SHM
πv/(b - a)
π(b - a)/ v
π(a - b)/v
(b - a)/πv
To solve the problem step by step, we need to analyze the motion of the body moving in simple harmonic motion (SHM) between points A and B.
Step 1: Understand the Setup
- The body moves along a straight line OAB.
- Points A and B are at distances 'a' and 'b' from point O, respectively.
- The body has zero velocity at points A and B.
- The body has velocity 'V' when it is halfway between A and B.
Step 2: Identify the Midpoint
- The midpoint (C) between A and B can be calculated as:
C=a+b2
- The distance between points A and B is:
d=b−a
Step 3: Relate Velocity to Amplitude
- In SHM, the maximum velocity Vmax occurs at the midpoint (C).
- The relationship between maximum velocity, angular frequency ω, and amplitude A is given by:
Vmax=ωA
- Here, A is the amplitude of the motion, which is half the distance between A and B:
A=d2=b−a2
Step 4: Relate Angular Frequency to Period
- The angular frequency ω is related to the period T by:
ω=2πT
- Substituting this into the maximum velocity equation gives:
Vmax=2πT⋅A
Step 5: Substitute for Amplitude
- Substitute A into the equation:
Vmax=2πT⋅b−a2
- Rearranging gives:
T=2π(b−a)2Vmax=π(b−a)Vmax
Step 6: Final Expression for Period
- Since the velocity at the midpoint is given as V, we can replace Vmax with V:
T=π(b−a)V
Conclusion
Thus, the period of the simple harmonic motion is:
T=π(b−a)V
- The body moves along a straight line OAB.
- Points A and B are at distances 'a' and 'b' from point O, respectively.
- The body has zero velocity at points A and B.
- The body has velocity 'V' when it is halfway between A and B.
- The midpoint (C) between A and B can be calculated as:
C=a+b2
- The distance between points A and B is:
d=b−a
- In SHM, the maximum velocity Vmax occurs at the midpoint (C).
- The relationship between maximum velocity, angular frequency ω, and amplitude A is given by:
Vmax=ωA
- Here, A is the amplitude of the motion, which is half the distance between A and B:
A=d2=b−a2
- The angular frequency ω is related to the period T by:
ω=2πT
- Substituting this into the maximum velocity equation gives:
Vmax=2πT⋅A
- Substitute A into the equation:
Vmax=2πT⋅b−a2
- Rearranging gives:
T=2π(b−a)2Vmax=π(b−a)Vmax
- Since the velocity at the midpoint is given as V, we can replace Vmax with V:
T=π(b−a)V
Thus, the period of the simple harmonic motion is:
T=π(b−a)V
Topper's Solved these Questions
Similar Questions
A simple pendulum executing SHM in a straight line has zero velocity at 'A' and 'B' whose distances form 'O' in the same line OAB are 'a' and 'b'. If the velocity half way between them is 'v' then its time period is
View SolutionTwo particles are moving along a straight line as shown. The velocity of approach between A and B is
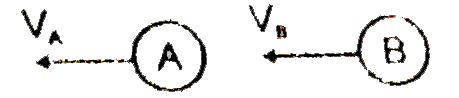
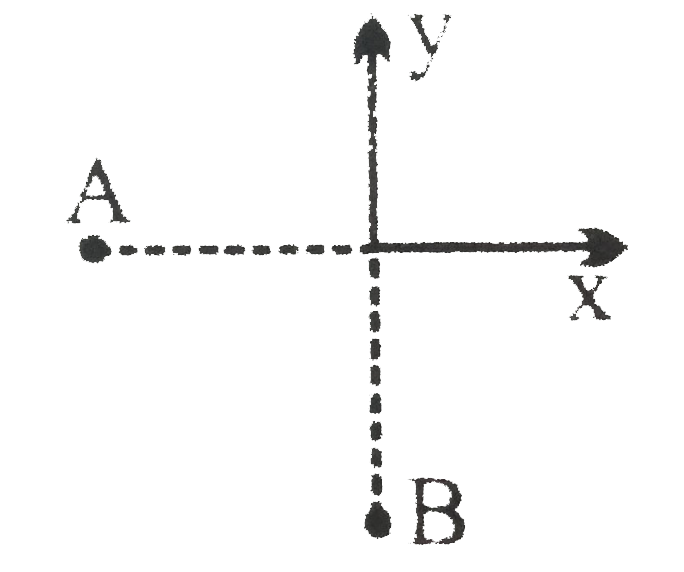
View SolutionParticles A and B are moving with constant velocities along x and y axis respectively, the graph of separation between them with time is
View SolutionA body is moving with constant acceleration, a=5ms2 from A to B in straight line AB. The velocity of particle at A and B are 5 m/s and 15 m/s respectively. The velocity at mid-point of AB is
View SolutionA particle is performing a linear simple harmonic motion. If the instantaneous acceleration and velocity of the particle are a and v respectively, identify the graph which correctly represents the relation between a and v.
View SolutionA body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph:
View SolutionA particle moving along a straight line with uniform acceleration has velocities 7m/s at A and 17m/s at C. B is the mid point of AC. Then :-
View SolutionFor a body moving with uniform acceleration along straight line, the variation of its velocity (v) with position (x) is best represented by
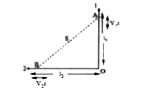
View SolutionTwo particles A and B move with constant velocity →v1 and →v2 along two mutually perpendicular straight lines towards intersection point O as shown in figure, At moment t = 0 particles were located at distance l1 and l2 respectively from O. Then minimu distance between the particles and time taken are respectively
View SolutionA particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are v1 and v2, respectively. Its time period is
View Solution
