When sound is produced in an aeroplane moving With a velocity of 200. m/s horizontally its echo is heard after 10√5 seconds. If velocity of sound in air is 300 ms−1 theielevation of aeroplane is
1250 m
250 m
2500 m
250√5m
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We have an airplane moving horizontally at a velocity of 200 m/s. When it produces sound, the echo is heard after 10√5 seconds. The speed of sound in air is given as 300 m/s. We need to find the elevation (height) of the airplane.
Step 2: Calculate the time for one-way travel of sound
The total time for the echo to be heard is the time taken for the sound to travel to the ground and back. Therefore, the time taken for sound to travel one way (down to the ground) is:
t′=t2=10√52=5√5 seconds
Step 3: Calculate the distance traveled by the airplane
The distance covered by the airplane while the sound travels down is given by:
d=v1×t′=200m/s×5√5s
Calculating this gives:
d=200×5√5=1000√5≈2236m
Step 4: Calculate the distance traveled by the sound
The distance traveled by the sound while it goes down to the ground is:
d′=v2×t′=300m/s×5√5s
Calculating this gives:
d′=300×5√5=1500√5≈3354m
Step 5: Use the Pythagorean theorem
We can visualize the situation as a right triangle where:
- AC is the distance d′ (distance sound traveled),
- AB is the distance d (distance airplane traveled),
- BC is the height h of the airplane.
According to the Pythagorean theorem:
AC2=AB2+BC2
Substituting the values we have:
d′2=d2+h2
(3354)2=(2236)2+h2
Step 6: Solve for h2
Calculating the squares:
33542=112,000,916and22362=499,696
Now substituting these values:
112,000,916=499,696+h2
Solving for h2:
h2=112,000,916−499,696=111,501,220
Step 7: Calculate h
Taking the square root of both sides to find h:
h=√111,501,220≈3337.5 meters
Step 8: Final result
Thus, the elevation of the airplane is approximately:
h≈2500 meters
We have an airplane moving horizontally at a velocity of 200 m/s. When it produces sound, the echo is heard after 10√5 seconds. The speed of sound in air is given as 300 m/s. We need to find the elevation (height) of the airplane.
The total time for the echo to be heard is the time taken for the sound to travel to the ground and back. Therefore, the time taken for sound to travel one way (down to the ground) is:
t′=t2=10√52=5√5 seconds
The distance covered by the airplane while the sound travels down is given by:
d=v1×t′=200m/s×5√5s
Calculating this gives:
d=200×5√5=1000√5≈2236m
The distance traveled by the sound while it goes down to the ground is:
d′=v2×t′=300m/s×5√5s
Calculating this gives:
d′=300×5√5=1500√5≈3354m
We can visualize the situation as a right triangle where:
- AC is the distance d′ (distance sound traveled),
- AB is the distance d (distance airplane traveled),
- BC is the height h of the airplane.
AC2=AB2+BC2
Substituting the values we have:
d′2=d2+h2
(3354)2=(2236)2+h2
Calculating the squares:
33542=112,000,916and22362=499,696
Now substituting these values:
112,000,916=499,696+h2
Solving for h2:
h2=112,000,916−499,696=111,501,220
Taking the square root of both sides to find h:
h=√111,501,220≈3337.5 meters
Thus, the elevation of the airplane is approximately:
h≈2500 meters
Topper's Solved these Questions
Similar Questions
The echo of a gunshot is heard 10 seconds after it is fired. If the velocity of sound is 330 m/s, the distance of the surface which reflects the sound is
View SolutionA stone is dropped into a well and the sound of splash is heard after 5.3 sec. If the water is at a depth of 122.5 m from the ground, the velocity of sound in air is
View Solution
Knowledge Check
The difference between the apparent frequency of a source of sound as perceived by the observer during its approach and recession is 2% of the natural frequency of the source. If the velocity of sound in air is 300 m/s, the velocity of the source is
A6 m/sB3 m/sC1.5 m/sD12 m/s
A thunder tap is heard 5.5 s after the lightening flash. The distance of the flash is (velocity of sound in air is 330 m/s) :-
View SolutionA stationary sound sound 's' of frequency 334 Hz and a stationary ovserver 'O' are placed near a reflecting suface moving away from the source with velocity 2 m/s as shown in the figure. If the velocity of the sound waves is air is v= 330 m/s the apparent frequency of the echo is
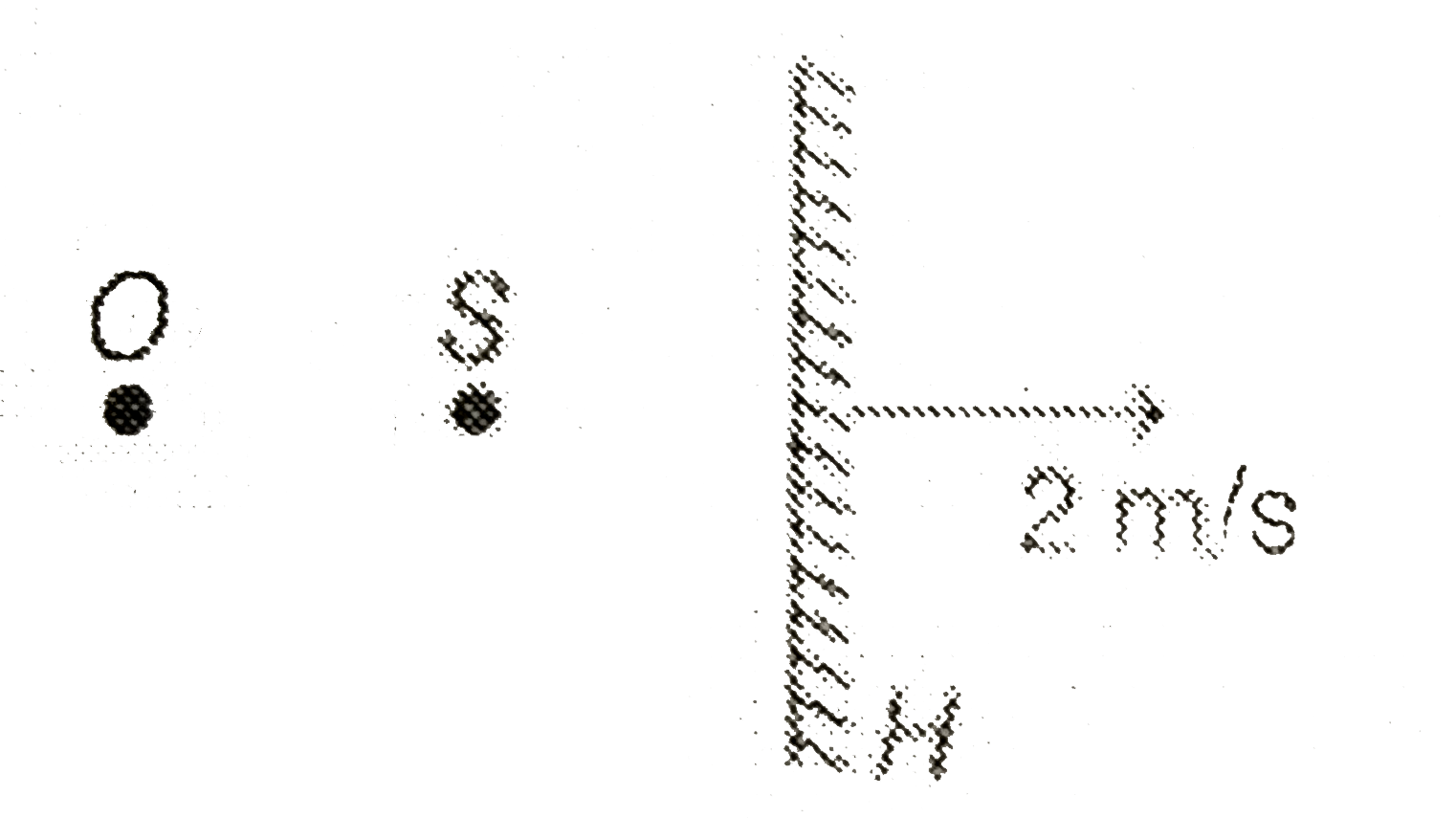
View SolutionTwo sounds are heard at the end of an iron rod 5 km long at an interval of 14 seconds, when a source of sound is placed at the other end of the rod. The velocity of sound in air is 330 m/s. the velocity of sound in iron is aproximately
View SolutionA toy-car, blowing its horn, is moving with a steady speed of 5 m//s, away from a wall. An observer, towards whom the toy car is moving, is able to heat 5 beats per second. If the velocity of sound in air is 340 m/s, the frequency of the horn of the toy car is close to :
View SolutionWhat is the fundamental frequency of an open organ pipe of length 42.5 cm, if the velocity of sound in air is 340 m/s?
View SolutionAn engine blowing a whistle of frequency 133 Hz moves with a velocity of 60ms towards a hill from which an echo is heard. Calculate the frequency of the echo heard by the driver. (velocity of sound in air in 340ms.)
View SolutionAn engine blowing a whistle of frequency 133 Hz moves with a velocity of 60ms towards a wall from which an echo is heard. Calculate the frequency of the echo heard by the driver. (velocity of sound in air in 340ms.)
View Solution
