A person feels 2.5% difference of frequency of a motor-car horn. If the motor-car is moving towards the person and the velocity of sound is 320 m/s, then the velocity of motor car will be (approximately)
80 m/s
8 cm/s
800 m/s
8 m/s
To solve the problem, we will use the Doppler effect formula for sound. Let's break down the solution step by step.
Step 1: Understand the Doppler Effect
The Doppler effect describes the change in frequency (or wavelength) of a wave in relation to an observer moving relative to the wave source. In this case, the motor-car horn is the source of sound, and the person is the observer.
Step 2: Define the Given Values
- The percentage difference in frequency is 2.5%.
- The velocity of sound (v) is 320 m/s.
- Let the original frequency of the horn be f.
- The observed frequency when the car is approaching is f′.
Step 3: Calculate the Observed Frequency
The observed frequency f′ can be expressed as:
f′=f+(2.5% of f)=f+0.025f=1.025f
Step 4: Use the Doppler Effect Formula
For a source moving towards a stationary observer, the Doppler effect formula is:
f′=f(vv−vs)
where:
- f′ is the observed frequency,
- f is the source frequency,
- v is the speed of sound,
- vs is the speed of the source (motor-car).
Step 5: Substitute the Known Values
Substituting f′=1.025f into the Doppler effect formula gives:
1.025f=f(320320−vs)
Step 6: Cancel f from Both Sides
Assuming f≠0, we can cancel f:
1.025=320320−vs
Step 7: Rearrange the Equation
Now, we can rearrange the equation to solve for vs:
1.025(320−vs)=320
Expanding the left side:
328−1.025vs=320
Step 8: Isolate vs
Now, isolate vs:
328−320=1.025vs
8=1.025vs
vs=81.025
Step 9: Calculate vs
Calculating vs:
vs≈7.8 m/s
Conclusion
Thus, the approximate velocity of the motor car is:
7.8 m/s
The Doppler effect describes the change in frequency (or wavelength) of a wave in relation to an observer moving relative to the wave source. In this case, the motor-car horn is the source of sound, and the person is the observer.
- The percentage difference in frequency is 2.5%.
- The velocity of sound (v) is 320 m/s.
- Let the original frequency of the horn be f.
- The observed frequency when the car is approaching is f′.
The observed frequency f′ can be expressed as:
f′=f+(2.5% of f)=f+0.025f=1.025f
For a source moving towards a stationary observer, the Doppler effect formula is:
f′=f(vv−vs)
where:
- f′ is the observed frequency,
- f is the source frequency,
- v is the speed of sound,
- vs is the speed of the source (motor-car).
Substituting f′=1.025f into the Doppler effect formula gives:
1.025f=f(320320−vs)
Assuming f≠0, we can cancel f:
1.025=320320−vs
Now, we can rearrange the equation to solve for vs:
1.025(320−vs)=320
Expanding the left side:
328−1.025vs=320
Now, isolate vs:
328−320=1.025vs
8=1.025vs
vs=81.025
Calculating vs:
vs≈7.8 m/s
Thus, the approximate velocity of the motor car is:
7.8 m/s
Topper's Solved these Questions
Similar Questions
A policeman on duty detects a drop of 10% in the pitch of the horn of a moving car as it crosses him. If the velocity of sound is 330m/s, the speed of the car will be
View SolutionA policeman on duty detects a drop of 10% in the pitch of the hom of a motor car as it crosses him. If the velocity of sound is 330 m/s calculate the speed of car?
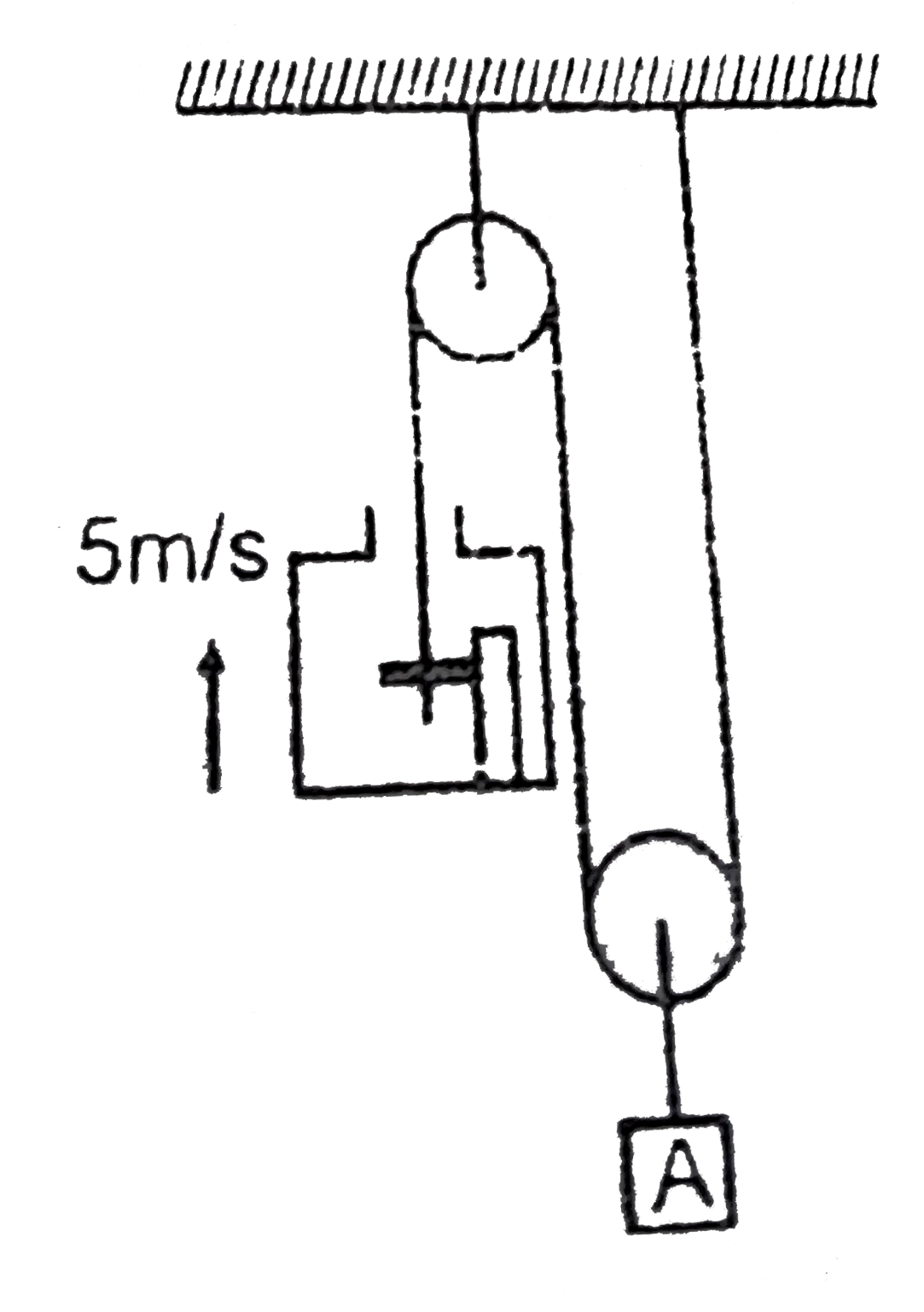
View SolutionA motor is fixed inside a box which is moving upwards with velocity 5m/s. String is winding at the rate 3m/s Then the velocity of block A will be.
View SolutionA car is moving towards a high cliff. The car driver sounds a horn of frequency f. The reflected sound heard by the driver has a frequency 2f. if v be the velocity of sound, then the velocity of the car, in the same velocity units, will be
View SolutionA car is moving towards a high cliff. The car driver sounds a horn of frequency f. The reflected sound heard by the driver has a frequency 2f. if v be the velocity of sound, then the velocity of the car, in the same velocity units, will be
View SolutionA toy-car, blowing its horn, is moving with a steady speed of 5 m//s, away from a wall. An observer, towards whom the toy car is moving, is able to heat 5 beats per second. If the velocity of sound in air is 340 m/s, the frequency of the horn of the toy car is close to :
View SolutionOut of the two cars A and B car A is moving towards east with velocity of 10 m/s whereas B is moving towards north with a velocity 20 m/s, then velocity of A w.r.t B is ( nearly )
View SolutionA car moving with constant acceleration crosses two points A and B with velocities 10 m/s and 20 m/s in its path. Find the velocity of the car midway between A and B. (in m/s).
View SolutionA person crossing a road with a certain velocity due north sees a car moving towards east The relative velocity of the car w.r.t the person is √2 times that fo the velocity of the persons. The angle made by the relative velocity with the east is
View SolutionA police car with a siren of frequency 8KHz is moving with uniform velocity 36Km/hr towards a ball building which reflects the sound waves. The speed of sound in air is 320m/s. The frequency of the siren heard by the car driver is
View Solution
