A string is rigidly tied at two ends and its equation of vibration is given by y = cos2πtsin2πx . Then minimum length of string is
1 m
5 m
0.5 m
2πm
To solve the problem, we need to find the minimum length of a string that is rigidly tied at both ends and has a given equation of vibration. The equation is:
y=cos(2πt)sin(2πx)
1. Understanding the Wave Equation:
The given equation represents a standing wave, which is formed by the superposition of two waves traveling in opposite directions. The general form of a standing wave can be written as:
y=Acos(2πft)sin(2πxλ)
where A is the amplitude, f is the frequency, t is time, x is position, and λ is the wavelength.
2. Identifying the Wavelength:
From the given equation, we can identify that:
sin(2πx)
corresponds to the term sin(2πxλ). By comparing the two, we see that:
2πxλ=2πx
This implies that:
λ=1 meter
3. Finding the Minimum Length of the String:
For a string fixed at both ends, the minimum length L that can support a standing wave is given by:
L=λ2
This is because the minimum standing wave pattern (fundamental frequency) consists of one loop, which is half of the wavelength.
4. Calculating the Minimum Length:
Substituting the value of λ:
L=1 meter2=0.5 meters
5. Conclusion:
Therefore, the minimum length of the string is:
0.5 meters
The given equation represents a standing wave, which is formed by the superposition of two waves traveling in opposite directions. The general form of a standing wave can be written as:
y=Acos(2πft)sin(2πxλ)
where A is the amplitude, f is the frequency, t is time, x is position, and λ is the wavelength.
From the given equation, we can identify that:
sin(2πx)
corresponds to the term sin(2πxλ). By comparing the two, we see that:
2πxλ=2πx
This implies that:
λ=1 meter
For a string fixed at both ends, the minimum length L that can support a standing wave is given by:
L=λ2
This is because the minimum standing wave pattern (fundamental frequency) consists of one loop, which is half of the wavelength.
Substituting the value of λ:
L=1 meter2=0.5 meters
Therefore, the minimum length of the string is:
0.5 meters
Topper's Solved these Questions
Similar Questions
A string is rigidly tied at two ends and its equation of vibration is given by y=cos2πx. Then minimum length of string is
View SolutionThe equation for the vibration of a string fixed at both ends vibrating in its second harmonic is given by y=2sin(0.3cm−1)xcos((500πs−1)t)cm. The length of the string is :
View SolutionA string is clamped at both the ends and it is vibrating in its 4th harmonic. The equation of the stationary wave is Y=0.3sin(0.157x)cos(200πt). The length of the string is : (All quantities are in SI units.)
View SolutionA uniform string is clamped at x=0 and x = L and is vibrating in its fundamental mode. Mass per unit length of the string is μ, tension in it is T and the maximum displacement of its midpoint is A. Find the total energy stored in the string. Assume to be small so that changes in tension and length of the string can be ignored
View SolutionA string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).

View SolutionA stone is tied to one end of a string and rotated in horizontal circle with a uniform angular velocity. The tension in the string is T, if the length of the string is halved and its angular velocity is doubled , the tension in the string will be
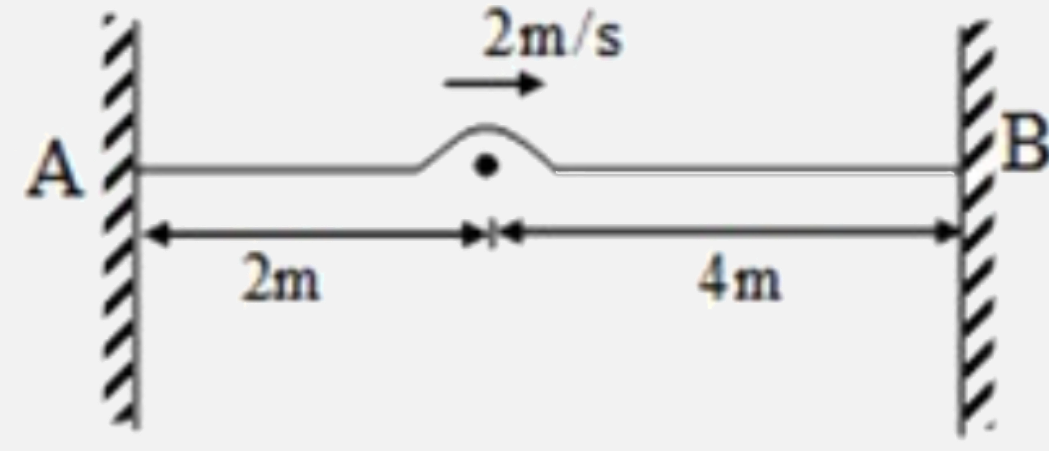
View SolutionA string is tied at two rigid supports . A pulse is generated on the string as shown in figure . Minimum time after which string will regain its shape as shown in figure ( Neglect the time during reflection )
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionA string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Minimum distance between the two points having amplitude 2 mm is:
View SolutionA string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Minimum distance between the two points having amplitude 2 mm is:
View Solution
