The two arms of a balanced are of unequal length. An object when placed in the left pan of the balance weighs 4 kg. The same object when placed in the right pan of the balance weighs 9 kg. The actual (or) true mass of the object is
To solve the problem, we need to analyze the situation with the balance and the weights involved. Let's break it down step by step.
Step 1: Understand the Setup
We have a balance with two pans of unequal lengths. When the object is placed in the left pan, it weighs 4 kg, and when placed in the right pan, it weighs 9 kg. We need to find the true mass (m) of the object.
Step 2: Set Up the Equations
1. Left Pan: When the object is in the left pan, the balance reads 4 kg. The weight on the left side can be expressed as:
m+w=4+w+x
Here, w is the weight of the left pan, and x is the additional weight due to the longer right pan.
2. Right Pan: When the object is in the right pan, the balance reads 9 kg. The weight on the left side can be expressed as:
9+w=m+w+x
Step 3: Simplify the Equations
From the first equation:
m+w=4+w+x
Subtract w from both sides:
m=4+x (Equation 1)
From the second equation:
9+w=m+w+x
Subtract w from both sides:
9=m+x (Equation 2)
Step 4: Solve the Equations
Now we have two equations:
1. m=4+x
2. 9=m+x
Substituting Equation 1 into Equation 2:
9=(4+x)+x
This simplifies to:
9=4+2x
Subtract 4 from both sides:
5=2x
Divide by 2:
x=2.5
Step 5: Find the True Mass
Now substitute x back into Equation 1 to find m:
m=4+2.5=6.5 kg
Conclusion
The actual (or true) mass of the object is 6.5 kg.
---
We have a balance with two pans of unequal lengths. When the object is placed in the left pan, it weighs 4 kg, and when placed in the right pan, it weighs 9 kg. We need to find the true mass (m) of the object.
1. Left Pan: When the object is in the left pan, the balance reads 4 kg. The weight on the left side can be expressed as:
m+w=4+w+x
Here, w is the weight of the left pan, and x is the additional weight due to the longer right pan.
9+w=m+w+x
From the first equation:
m+w=4+w+x
Subtract w from both sides:
m=4+x (Equation 1)
9+w=m+w+x
Subtract w from both sides:
9=m+x (Equation 2)
Now we have two equations:
1. m=4+x
2. 9=m+x
9=(4+x)+x
This simplifies to:
9=4+2x
Subtract 4 from both sides:
5=2x
Divide by 2:
x=2.5
Now substitute x back into Equation 1 to find m:
m=4+2.5=6.5 kg
The actual (or true) mass of the object is 6.5 kg.
Topper's Solved these Questions
Similar Questions
A physical balance has its arms of unequal length. A body weight 18 kg if kept in one pan and weight 8 kg. If kept in the other pan. The true weight of the body is
View SolutionA body weighs 6gms when placed in one pan and 24gms when placed on the other pan of a false balance. If the beam is horizontal when both the pans are empty, the true weight of the body is :
View SolutionA beam balance of unequal arm length is used by an unscruplus trader. When an object is weighed on left pan. The weight i found to be W1. When the object is weighed on the right plane, the weight is found to be W2. If W1≠W2, the correct weight of the object is
View SolutionA physical balance has its arms of length 60cm and 40cm. What weight kept on the pan of the longer arm will balance an object of weight 100 gf kept on the other pan?
View SolutionIn a physical balance working on the principle of moments, when 5 mg weight is placed on the left pan, the beam becomes horizontal. Both the empty pans of the balance are of equal mass. Which of the following statements is correct ?
View SolutionIn a physical balance working on the principle of moments, when 5 mg weight is placed on the left pan, the beam becomes horizontal. Both the empty pans of the balance are of equal mass. Which of the following statements is correct ?
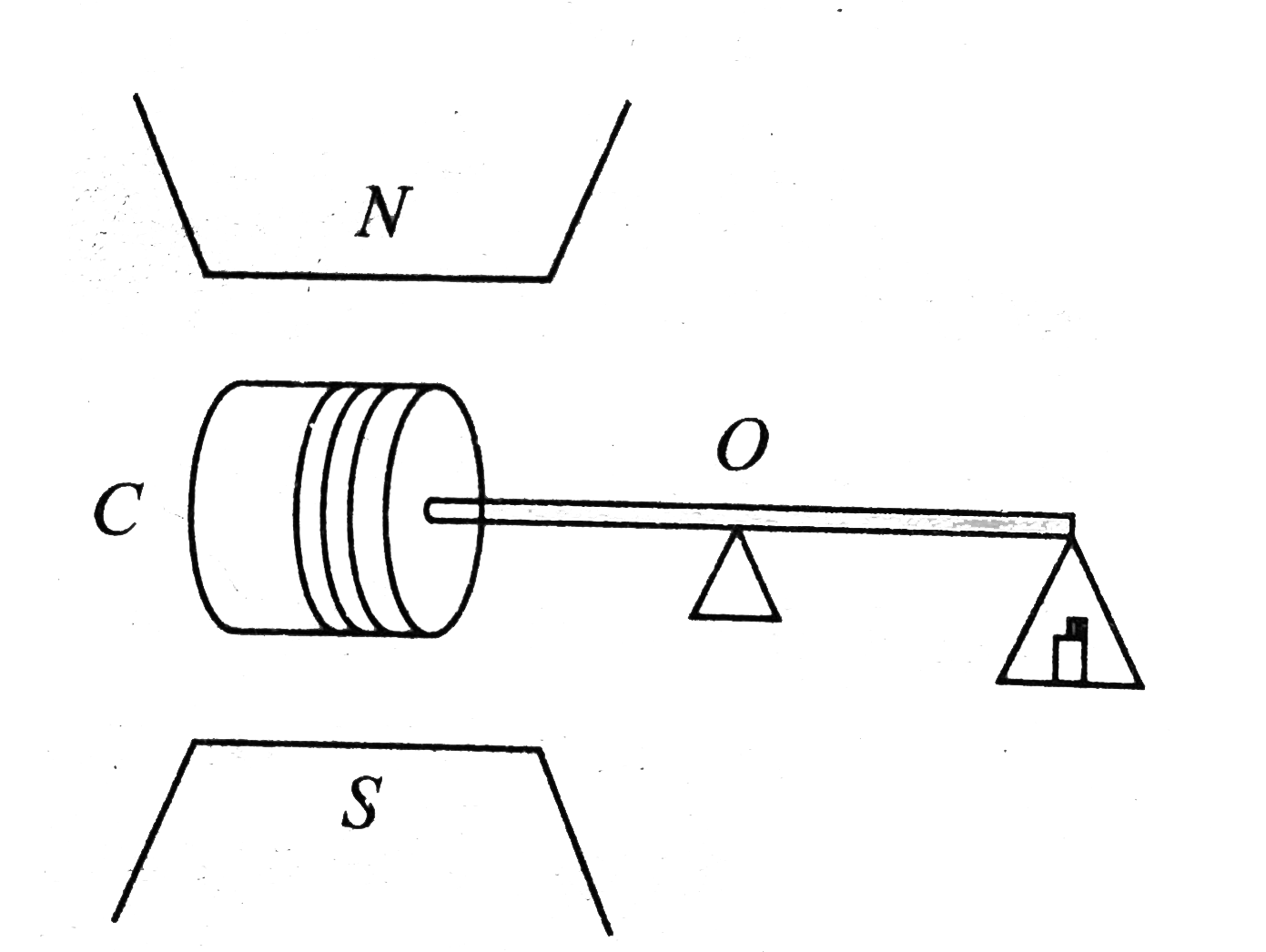
View SolutionA small coil C with N=200 turns is mounted on one end of a balance beam and introduced between the poles of an electromagnetic as shown in Fig. The area of the coils is S=1cm2, the length of the right arm of the balance beam is l=30cm. When there is no current in the coil the balance is in equilibrium. On passing is a currentI=22mA through the coil, equilibrium is restored by putting an additional weight of mass m=60mg on the balance pan. Find the magnetic induction field (in terms of x10−1T) between the poles of the electromagnetic assuming it to be uniform.
View SolutionFigure shows a light spring balance connected to two blocks of mass 20 kg each. The graduations in the balance measure the tension in the spring. A. What is the reading of the balance? B. Will the reading change if the balance is heavy, say 2.0 kg? c. What will happen if the spring is light but the blocks have unequal masses?

View SolutionWhen an object is placed between two parallel mirrors, then number of images formed are
View SolutionWhen the two plane mirror are parallel to each other, then the number of images of an object placed between them is
View Solution
