A beam balance of unequal arm length is used by an unscruplus trader. When an object is weighed on left pan. The weight i found to be W1. When the object is weighed on the right plane, the weight is found to be W2. If W1≠W2, the correct weight of the object is
W1+W22
√W1W2
√W21+W22
√W22−W21
The correct Answer is:B
To find the correct weight of the object using a beam balance of unequal arm lengths, we can follow these steps:
Step 1: Understand the System
We have a beam balance with two pans of unequal lengths. Let:
- W = actual weight of the object
- W1 = weight measured when the object is on the left pan
- W2 = weight measured when the object is on the right pan
- r1 = length of the left arm
- r2 = length of the right arm
Step 2: Set Up the Moment Equations
When the object is placed on the left pan, the balance is in equilibrium, which gives us:
W⋅r1=W1⋅r2(1)
This equation states that the moment produced by the actual weight on the left side is equal to the moment produced by the weight W1 on the right side.
When the object is placed on the right pan, we have:
W2⋅r1=W⋅r2(2)
This equation states that the moment produced by the weight W2 on the left side is equal to the moment produced by the actual weight W on the right side.
Step 3: Solve the Equations
From equation (1):
W=W1⋅r2r1
From equation (2):
W=W2⋅r1r2
Step 4: Equate the Two Expressions for W
Setting the two expressions for W equal to each other:
W1⋅r2r1=W2⋅r1r2
Step 5: Cross Multiply
Cross multiplying gives us:
W1⋅r22=W2⋅r21
Step 6: Express the Actual Weight
Now, we can express the actual weight W in terms of W1 and W2:
W=√W1⋅W2
Conclusion
Thus, the correct weight of the object is:
W=√W1⋅W2
---
We have a beam balance with two pans of unequal lengths. Let:
- W = actual weight of the object
- W1 = weight measured when the object is on the left pan
- W2 = weight measured when the object is on the right pan
- r1 = length of the left arm
- r2 = length of the right arm
When the object is placed on the left pan, the balance is in equilibrium, which gives us:
W⋅r1=W1⋅r2(1)
This equation states that the moment produced by the actual weight on the left side is equal to the moment produced by the weight W1 on the right side.
W2⋅r1=W⋅r2(2)
This equation states that the moment produced by the weight W2 on the left side is equal to the moment produced by the actual weight W on the right side.
From equation (1):
W=W1⋅r2r1
From equation (2):
W=W2⋅r1r2
Setting the two expressions for W equal to each other:
W1⋅r2r1=W2⋅r1r2
Cross multiplying gives us:
W1⋅r22=W2⋅r21
Now, we can express the actual weight W in terms of W1 and W2:
W=√W1⋅W2
Thus, the correct weight of the object is:
W=√W1⋅W2
Similar Questions
If equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
View SolutionThe two arms of a balanced are of unequal length. An object when placed in the left pan of the balance weighs 4 kg. The same object when placed in the right pan of the balance weighs 9 kg. The actual (or) true mass of the object is
View SolutionThe weight of an object in the coal mine, sea level and at the top of the mountain are W1,W2 and W3 respectively, then
View SolutionAn object weighs 10 N in air. When immessed fully in liquid, it weighs only 8 N. The weight of the liquid displaced by the object will be:
View SolutionAn object weigh 10 N when measured on the surface of the earth. What would be its weight when measure on the surface of moon ?
View SolutionA physical balance has its arms of length 60cm and 40cm. What weight kept on the pan of the longer arm will balance an object of weight 100 gf kept on the other pan?
View SolutionIn meter bridge , the balancing length from left is found to be 20 cm when standard connected of 1Ω is in right gap . The value of unknown resistance is
View SolutionThe Price relative and weight of a set of commoditities are given in the following table
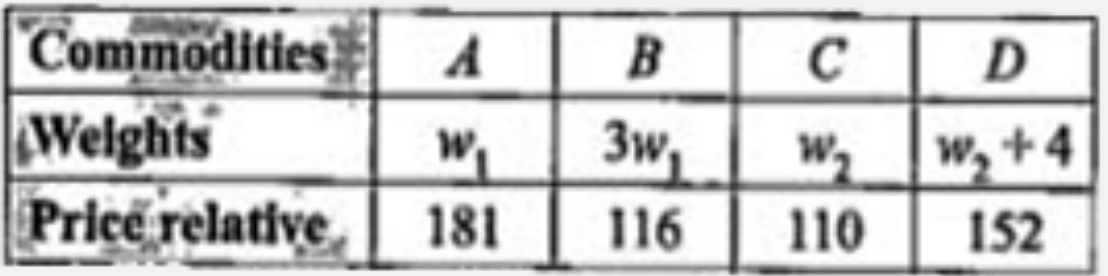
If the index for the set is 135 and the sum of the weight is 26, find w1+w2
View SolutionTwo wires W1andW2 have the same radius r and respective densities p1andp2 such that p2=4p1. They are joined together at the point O, as shown in the figure. The combination is used as a sonometer wire and kept udner tension T. The point O is midway between the two bridges. When a stationary waves is set up in the composite wire, the joint is found to be a node. The ratio of the number of antinodes formed in W1toW2 is-

View SolutionTwo wires W1andW2 have the same radius r and respective densities p1andp2 such that p2=4p1. They are joined together at the point O, as shown in the figure. The combination is used as a sonometer wire and kept udner tension T. The point O is midway between the two bridges. When a stationary waves is set up in the composite wire, the joint is found to be a node. The ratio of the number of antinodes formed in W1toW2 is-

View Solution
