A small metallic bob of mass m of a simple pendulum of length L is suspended between the two oppositely charged large parallel plates . The electric field E act vertically. If positive charge 'q' is given to bob and displaced slightly from mean position then time period of oscillation will be
A. when lower plate charge positively
B. when lower plate charge negetively
C. when lower plate charge negetively
D. both a and c
To find the time period of oscillation of a small metallic bob of mass m suspended between two oppositely charged parallel plates in an electric field E, we can follow these steps:
Step 1: Understand the Forces Acting on the Bob
The bob experiences two main forces:
1. The gravitational force acting downwards: Fg=mg
2. The electric force acting upwards due to the electric field: Fe=qE
Step 2: Set Up the Equation of Motion
When the bob is displaced slightly from its mean position, the net force acting on it can be expressed as:
Fnet=mg−qE
This net force will cause the bob to accelerate. According to Newton's second law, we have:
ma=mg−qE
Where a is the acceleration of the bob.
Step 3: Calculate the Effective Acceleration
Rearranging the equation gives us:
a=g−qEm
Let’s denote the effective acceleration due to gravity in the presence of the electric field as g′:
g′=g−qEm
Step 4: Write the Expression for Time Period
The time period T of a simple pendulum is given by:
T=2π√Lg′
Substituting g′ into the equation gives:
T=2π
⎷Lg−qEm
Step 5: Final Expression for Time Period
Thus, the final expression for the time period of oscillation of the bob is:
T=2π
⎷Lg−qEm
The bob experiences two main forces:
1. The gravitational force acting downwards: Fg=mg
2. The electric force acting upwards due to the electric field: Fe=qE
When the bob is displaced slightly from its mean position, the net force acting on it can be expressed as:
Fnet=mg−qE
This net force will cause the bob to accelerate. According to Newton's second law, we have:
ma=mg−qE
Where a is the acceleration of the bob.
Rearranging the equation gives us:
a=g−qEm
Let’s denote the effective acceleration due to gravity in the presence of the electric field as g′:
g′=g−qEm
The time period T of a simple pendulum is given by:
T=2π√Lg′
Substituting g′ into the equation gives:
T=2π
⎷Lg−qEm
Thus, the final expression for the time period of oscillation of the bob is:
T=2π
⎷Lg−qEm
Similar Questions
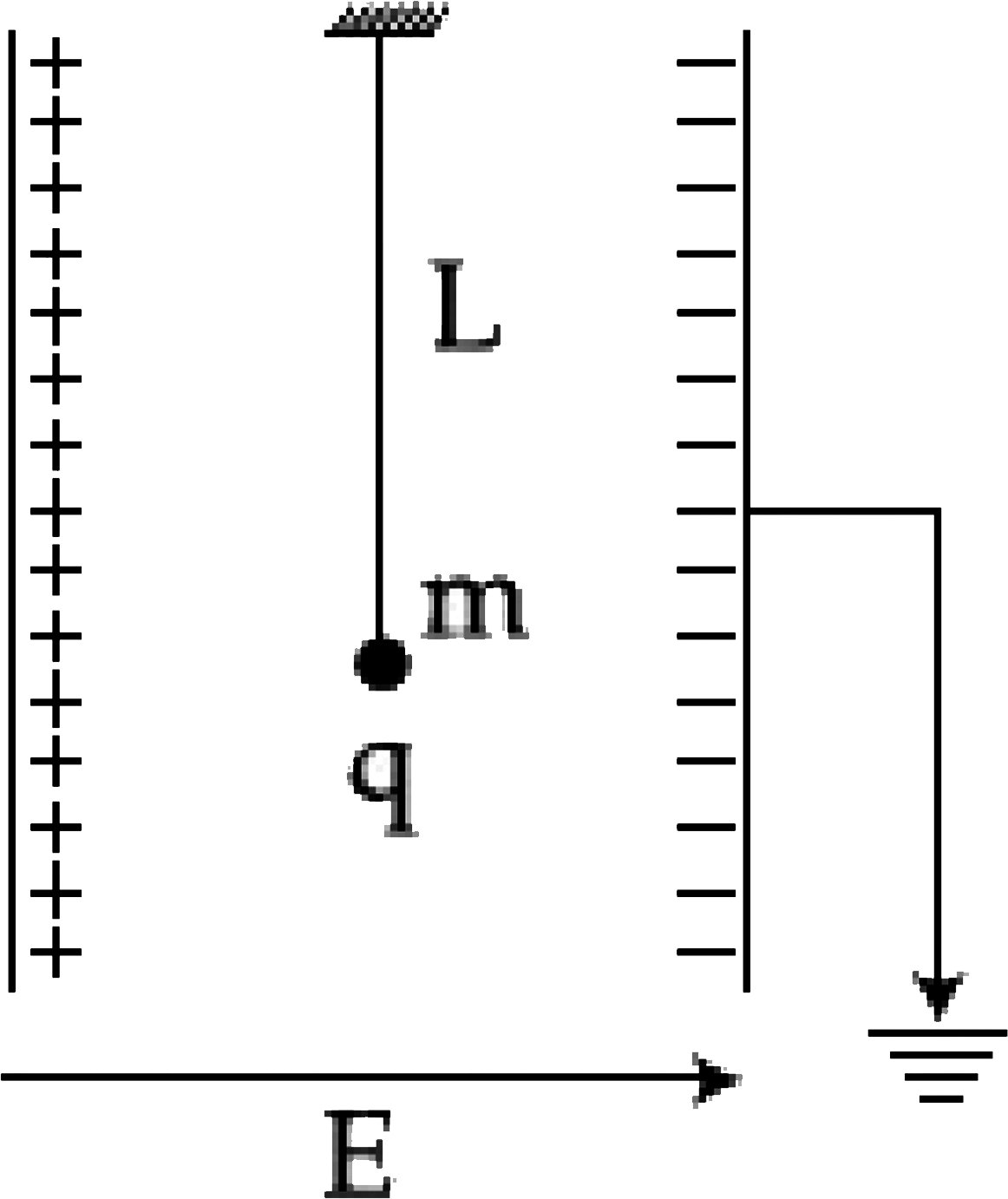
A simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:
View SolutionA simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:
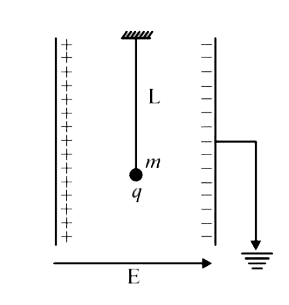
View SolutionA simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:

View SolutionA neutral pendulum oscillates in a uniform electric field as shown in figure. If a positive charge is given to the pendulum, then its time period

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionThe bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View SolutionThe bob of a simple pendulum of length /has a positive charge q on it. The pendulum is fixed to a horizontally oriented positively charged sheet as shown in the figure. The time period of the small oscillations of simple pendulum is
View SolutionA pendulum of length L carries a negative charge - q on the bob. A positive charge +q is held at the point of support . Then, the time period of the bob is
View SolutionWhat is the torque acting on the bob of mass m of a simple pendulum Of length l, when the string of the pendulum makes an angle θ with the vertical ? When is the torque (i) zero and (ii) maximum.
View SolutionAn electric dipole of dipole moment p is placed in a uniform electric field E in stable equilibrium position. Its moment of inertia about the centroidal axis is I . If it is displaced slightly from its mean position, find the period of small oscillations.
View Solution