The bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
lθ0cos√glt
l√gltcosθ0
lgsinθ0
lθ0sin√glt
The correct Answer is:A
To solve the problem of finding the linear displacement of a simple pendulum bob released from a small angular displacement, we can follow these steps:
1. Understand the Pendulum Setup:
- A simple pendulum consists of a mass (bob) attached to a string of length L.
- When the bob is displaced to an angle θ0 and released, it will undergo simple harmonic motion (SHM).
2. Equation of Motion:
- The angular displacement θ of the pendulum as a function of time t can be expressed as:
θ(t)=θ0cos(ωt)
- Here, θ0 is the initial angular displacement, and ω is the angular frequency.
3. Determine the Angular Frequency:
- The angular frequency ω for a simple pendulum is given by:
ω=√gL
- Where g is the acceleration due to gravity.
4. Linear Displacement:
- The linear displacement x of the bob from the vertical position can be related to the angular displacement by:
x=Lθ
- Substituting the expression for θ(t):
x(t)=Lθ0cos(ωt)
5. Final Expression for Linear Displacement:
- Now substituting ω into the equation:
x(t)=Lθ0cos(√gLt)
Conclusion:
The linear displacement of the pendulum bob at time t is given by:
x(t)=Lθ0cos(√gLt)
- A simple pendulum consists of a mass (bob) attached to a string of length L.
- When the bob is displaced to an angle θ0 and released, it will undergo simple harmonic motion (SHM).
- The angular displacement θ of the pendulum as a function of time t can be expressed as:
θ(t)=θ0cos(ωt)
- Here, θ0 is the initial angular displacement, and ω is the angular frequency.
- The angular frequency ω for a simple pendulum is given by:
ω=√gL
- Where g is the acceleration due to gravity.
- The linear displacement x of the bob from the vertical position can be related to the angular displacement by:
x=Lθ
- Substituting the expression for θ(t):
x(t)=Lθ0cos(ωt)
- Now substituting ω into the equation:
x(t)=Lθ0cos(√gLt)
The linear displacement of the pendulum bob at time t is given by:
x(t)=Lθ0cos(√gLt)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II
1 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - III
12 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - II
36 Videos
- SEMICONDUCTORSBOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 3
88 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS
784 Videos
Similar Questions
A simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
View SolutionIf the metal bob of a simple pendulum is replaced by a wooden bob, then its time period will
View SolutionA simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
View SolutionA simple pendulum of mass 'm' , swings with maximum angular displacement of 60∘ . When its angular displacement is 30∘ ,the tension in the string is
View SolutionA simple pendulum of length L and mass M is oscillating about a vertical line with angular amplitude θ. If for an angular displacement ϕ(ϕ>θ) the tension in the string is T1 and for angular amplitude θ the tension is T2, then
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.
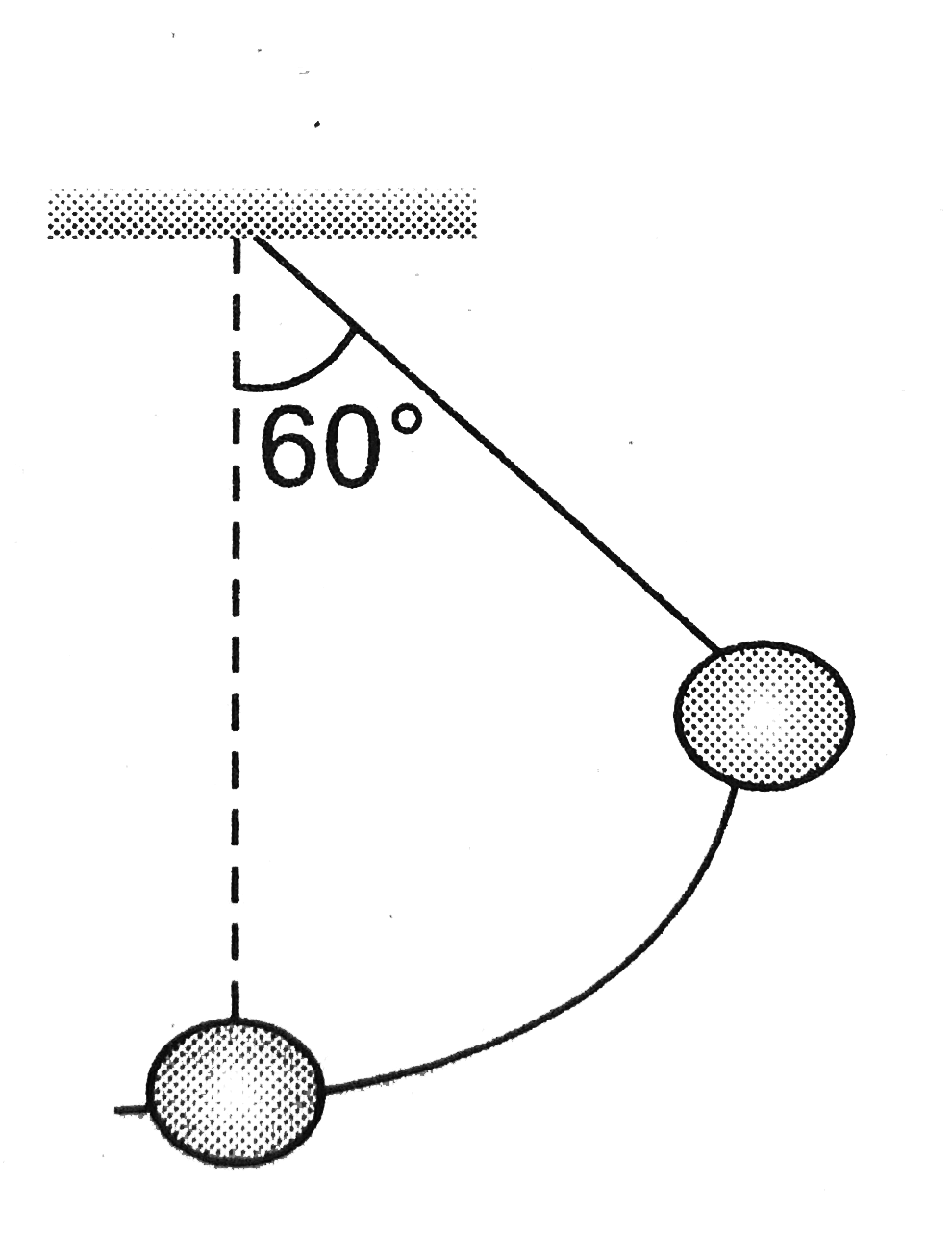
View SolutionA pendulum of length l=1m is released from θ0=60∘ . The rate of change of speed of the bob at θ=30∘ is.

View SolutionThe matallic bob of a simple pendulum has the relative density ρ. The time period of this pendulum is T it the metallic bob is immersed in water the new time period is given by
View SolutionThe matallic bob of a simple pendulum has the relative density ρ. The time period of this pendulum is T it the metallic bob is immersed in water the new time period is given by
View SolutionTwo simple pendulums of length 0.5 m and 20 m, respectively are given small linear displacement in one direction at the same time. They will again be in the phase when the pendulum of shorter length has completed oscillations.
View Solution
