A block of mass is connected with a spring having spring constant N/m held in equilibrium between two vertical walls 'A' and 'B' as shown as in figure.If compression in the spring is cm and all the surfaces are smooth then normal reaction by the block on the wall B' will be
N
N
N
N
To solve the problem, we need to determine the normal reaction force exerted by the block on wall B when the spring is compressed. Here's a step-by-step solution:
Step 1: Understand the Given Data
- Mass of the block (m) = 2 kg
- Spring constant (k) = 200 N/m
- Compression in the spring (x) = 4 cm = 0.04 m (convert cm to m for calculations)
Step 2: Calculate the Force Exerted by the Spring
The force exerted by a spring when compressed or stretched is given by Hooke's Law:
F=k⋅x
Where:
- F is the force exerted by the spring,
- k is the spring constant,
- x is the compression or extension of the spring.
Substituting the values:
F=200N/m⋅0.04m
Step 3: Perform the Calculation
Calculating the force:
F=200⋅0.04=8N
Step 4: Determine the Normal Reaction Force
In equilibrium, the normal reaction force (N) exerted by the block on wall B will be equal to the force exerted by the spring. Thus:
N=F
So,
N=8N
Conclusion
The normal reaction by the block on wall B is 8N.
---
- Mass of the block (m) = 2 kg
- Spring constant (k) = 200 N/m
- Compression in the spring (x) = 4 cm = 0.04 m (convert cm to m for calculations)
The force exerted by a spring when compressed or stretched is given by Hooke's Law:
F=k⋅x
Where:
- F is the force exerted by the spring,
- k is the spring constant,
- x is the compression or extension of the spring.
F=200N/m⋅0.04m
Calculating the force:
F=200⋅0.04=8N
In equilibrium, the normal reaction force (N) exerted by the block on wall B will be equal to the force exerted by the spring. Thus:
N=F
So,
N=8N
The normal reaction by the block on wall B is 8N.
Similar Questions
A block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
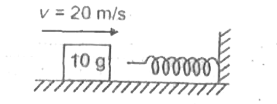 View Solution
View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:
 View Solution
View SolutionA block of mass 20 kg is hung with the help of ideal string, pulleys and spring (Spring constant k = 1000 N/m) as shown in figure. If block is in equilibrium position then extension in the spring will be (g=10ms−2)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural lengthView SolutionTwo blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
View SolutionA block of mass m is connected to a spring of spring constant k as shown in figure. The frame in which the block is placed is given an acceleration a towards left. Neglect friction between the block and the frame walls. The maximum velocity of the block relative to the frame is
 View Solution
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass m is connected two springs of spring constant 2k annd k , respectively , as shown in the vertical plane. At equilibrium , both springs are compressed by same length. If suddenly lower spring is cut, then acceleration of block, just after spring cut , is
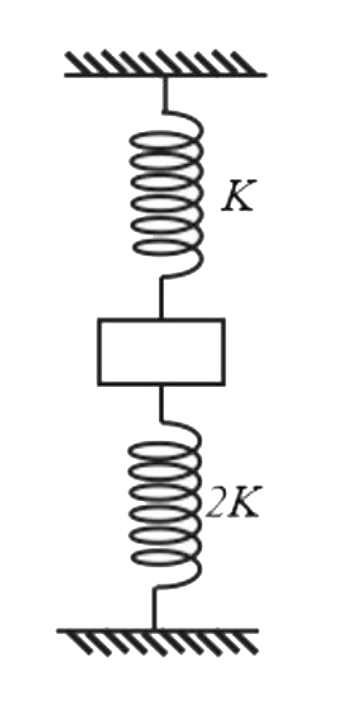 View Solution
View SolutionA block of mass m is moving with an initial velocity v0 towards a stationary spring of stiffness k attached to the wall as shown in figure

a. Find the maximum compression in the spring.
b. Is the work done by the spring negative or positive?View Solution

