Question

The block of mass M in figure $-4.160,$ initially has a velocity $v_o$ to the right and its positionis much that the spring exerts no froce on it, i.e, the spring is not stretched or comkpressed. The block moves to the right a distance l before sttoping in the dotted position shown. The speing constant is k and the coefficeent of kinetic friction between block and table is $\mu .$ as the block moves the distance l, (a) what is the work done on it by the friction force ? (b) What is the work done on it by the spring force ? (c) are there other forces actionon the block, and if so what work do they do ? (d) what is the total work done on the block?

Explanation

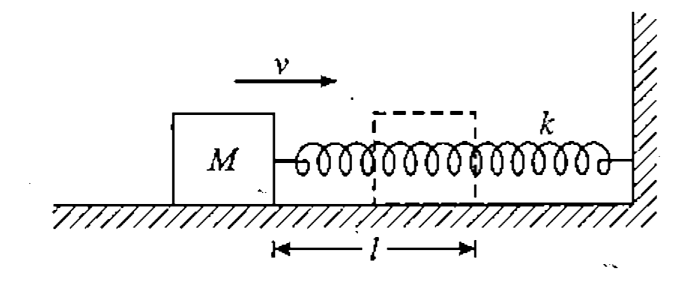
(a) The net force acting on the block by the spring is equal to `F_("spring")=kx`
Work done by the spring `= int vec(F)_("spring").d vec(s)`
`= int F_("spring") ds cos 180^(@)=- int F_("spring").ds`
`= - int_(0)^(l)kxdx=(-kl^(2))/(2)`

(b) The total work done `W=Delta KE=0-(1/2)mv_(0)^(2)=-(1/2)mv_(0)^(2)`.
(c) The work done by friction `= - mu mgl`
`rArr ` The total work done `W_(s)+W_(f)=DeltaKE=- mu mgl-(1//2)kl^(2)=-(1/2)mv_(0)^(2)`
`rArr 1/2 kl^(2)+mu mgl=1/2 mv_(0)^(2)`
`rArr l=(mu mg)/(k) [ sqrt(1+k/m ((v_(0))/(mu g))^(2))-1]`