A bomb is projected obliquely upward. It explodes at its highest point such that the pieces fly off with same speed in different directions in same vertical plane. Consider motion of the pieces of the bomb before they strike the ground
centre of mass of the system of pieces of the bomb follows straight path
centre of mass of the system of pieces of the bomb follows the same parabolic path
All the pieces lie on a circle at any instant
All the pieces lie on a parabola at any instant
To solve the problem step by step, we will analyze the motion of the bomb and its pieces after the explosion.
Step 1: Understanding the Initial Motion
The bomb is projected obliquely upward at an angle θ with respect to the horizontal. This means that it has both horizontal and vertical components of velocity. The motion of the bomb can be described as a projectile motion.
Hint: Remember that in projectile motion, the horizontal and vertical motions are independent of each other.
Step 2: Identifying the Highest Point
At the highest point of its trajectory, the vertical component of the bomb's velocity becomes zero, while the horizontal component remains unchanged. This is the point where the bomb explodes.
Hint: The highest point is where the vertical velocity is zero, and the bomb has maximum height.
Step 3: Analyzing the Explosion
When the bomb explodes at its highest point, the pieces fly off with the same speed but in different directions within the same vertical plane. This means that the explosion does not impart any additional horizontal velocity to the pieces; they will retain the horizontal component of velocity that the bomb had just before the explosion.
Hint: The pieces maintain the horizontal velocity of the bomb at the moment of explosion.
Step 4: Motion of the Center of Mass
Since no external forces act on the bomb during the explosion, the motion of the center of mass of the bomb system remains unaffected. The center of mass will continue to follow the same parabolic trajectory that the bomb was following before the explosion.
Hint: The principle of conservation of momentum applies here; the center of mass moves in the same way as it did before the explosion.
Step 5: Conclusion
As a result, the pieces of the bomb will follow a parabolic path, just like the bomb did before it exploded. Therefore, the correct answer to the question is that the center of mass of the system of pieces of the bomb follows the same parabolic path.
Hint: The trajectory of the center of mass is crucial in determining the overall motion of the system after the explosion.
Final Answer
The motion of the pieces of the bomb before they strike the ground follows the same parabolic path as the bomb itself.
The bomb is projected obliquely upward at an angle θ with respect to the horizontal. This means that it has both horizontal and vertical components of velocity. The motion of the bomb can be described as a projectile motion.
At the highest point of its trajectory, the vertical component of the bomb's velocity becomes zero, while the horizontal component remains unchanged. This is the point where the bomb explodes.
When the bomb explodes at its highest point, the pieces fly off with the same speed but in different directions within the same vertical plane. This means that the explosion does not impart any additional horizontal velocity to the pieces; they will retain the horizontal component of velocity that the bomb had just before the explosion.
Since no external forces act on the bomb during the explosion, the motion of the center of mass of the bomb system remains unaffected. The center of mass will continue to follow the same parabolic trajectory that the bomb was following before the explosion.
As a result, the pieces of the bomb will follow a parabolic path, just like the bomb did before it exploded. Therefore, the correct answer to the question is that the center of mass of the system of pieces of the bomb follows the same parabolic path.
The motion of the pieces of the bomb before they strike the ground follows the same parabolic path as the bomb itself.
Similar Questions
Two particles AandB are projected from the same point in different directions in such a manner that vertical components of their initial velocities are same (Fig. 5.8). Find the ratio of range.
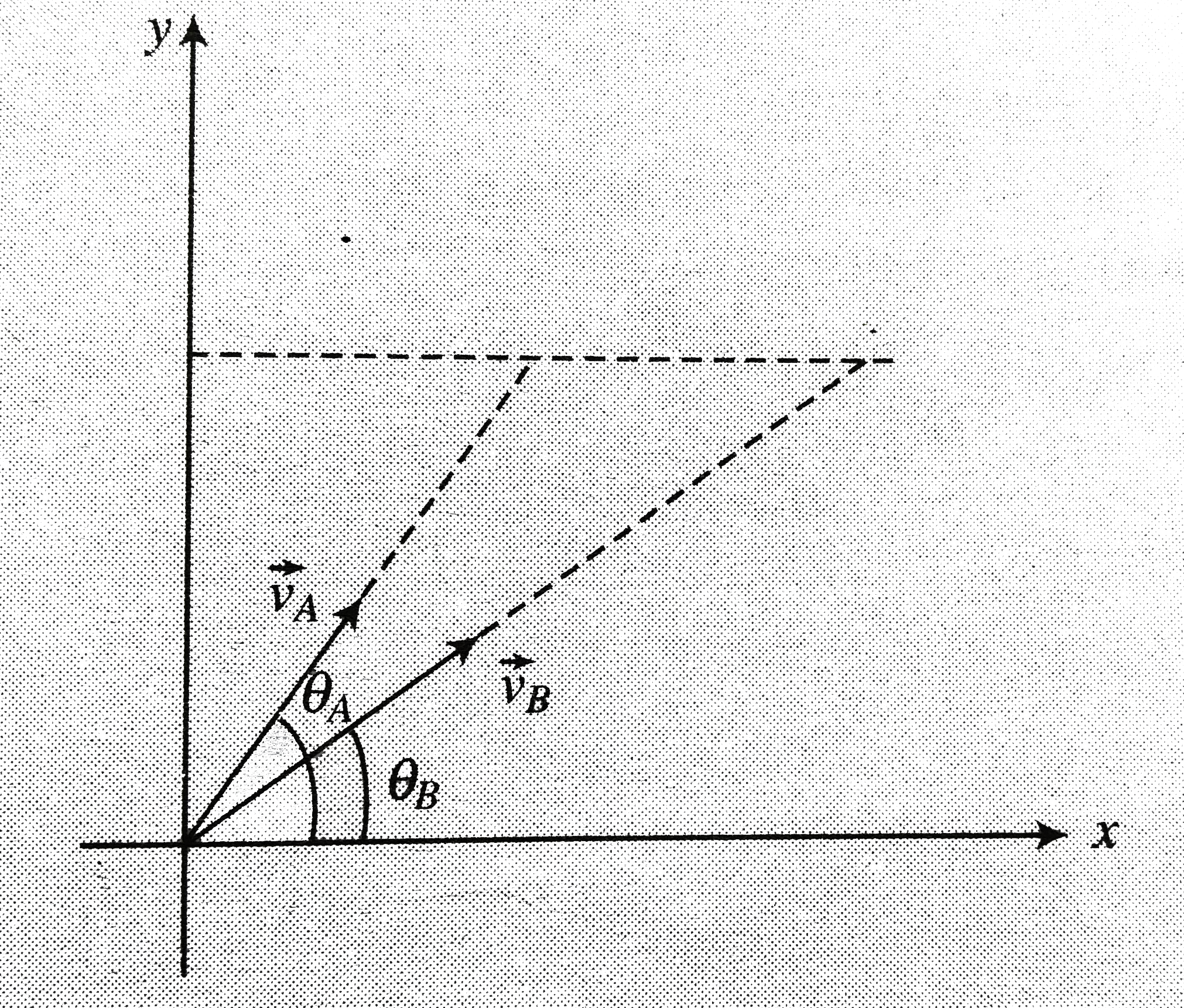 .View Solution
.View SolutionA particle of mass m is projected from origin O with speed u at an angle θ with positive x-axis. Positive y-axis is in vertically upward. Direction. Find the angular momentum of particle at any time t about O before the particle strikes the ground again.
View SolutionTwo bodies are projected from the same point with equal velocities in such a directions that they strike on the same point on a plane whose inclination is β. If α is the angle of projection of the first , the ratio of there times of flight is
View SolutionThere are two identical particles A and B. One is projected vertically upward with speed √2gh from ground and other is dropped from height h along the same vertical line. Collision between them is perfectly inelastic. Find time taken by them to reach the ground after collision in terms of √hg.
View SolutionA body is projected vertically upward with speed 10m/s and other at same time with same speed in downward direction from the top of a tower. The magnitude of acceleration of first body w.r.t. second is {take g=10m/s2}
View SolutionA bomb is projected with speed 10 m/s at an angle 30o with the horizontal. In the mid-air bomb explodes in different fragments and they all move in different directions. At the time when all fragments reach at ground, the displacement of the center of mass of bomb from initial point will be (g = 10 m/s2)
View SolutionA ball is projected vertically upwards with a certain initial speed. Another ball of the same mass is projected at an angle of 60∘ with the vertical with the same initial speed. At highest points of their journey, the ratio of their potential energies will be
View SolutionA ball is projected vertically upwards with a certain initial speed. Another ball of the same mass is projected at an angle of 60∘ with the vertical with the same initial speed. At highest points of their journey, the ratio of their potential energies will be
View SolutionAssertion:- Two stones are simultaneously projected from level ground from same point with same speeds but different angles with horizontal Both stones move in same vertical plane. Then the two stones may collide in mid air.
Reason:- For two stones projected simultaneously from same point with same speed at different angles with horizontal, their trajectories must intersect at some point except projection point.View SolutionA projectile of mass 3m is projected from ground with velocity 20√2m/s at 45∘. At highest point it explodes into two pieces. One of mass 2m and the other of mass m. Both the pieces fly off horizontally in opposite directions. Mass 2m falls at a distance of 100m from point of projection. Find the distance of second mass from point of projection where it strikes the ground.
(g=10m/s2)View Solution

