A particle of mass m and charge q is oscillating simple harmonically from a string of length l.Now a vertical electric field of magnitude E=mg2q is switched on.The ration of new time period to old time period is
A. 2:1
B. 1:2
C. √2:1
D. 1:1
To solve the problem, we will follow these steps:
Step 1: Understand the scenario
A particle of mass m and charge q is oscillating in simple harmonic motion (SHM) from a string of length l. When a vertical electric field of magnitude \( E = \frac{mg}{2q} \) is applied, we need to find the ratio of the new time period to the old time period of the oscillation.
Step 2: Determine the force due to the electric field
The force \( F \) on the particle due to the electric field \( E \) is given by:
\(
F = qE
\)
Substituting the value of \( E \):
\(
F = q \left(\frac{mg}{2q}\right) = \frac{mg}{2}
\)
Here, the charge \( q \) cancels out.
Step 3: Calculate the effective acceleration
The effective force acting on the particle is the gravitational force minus the force due to the electric field:
\(
F_{\text{effective}} = mg - \frac{mg}{2} = \frac{mg}{2}
\)
Thus, the effective acceleration \( g_{\text{eff}} \) acting on the particle is:
\(
g_{\text{eff}} = \frac{mg_{\text{effective}}}{m} = \frac{g}{2}
\)
Step 4: Write the formula for the time period
The time period \( T \) of a simple harmonic oscillator is given by:
\(
T = 2\pi \sqrt{\frac{l}{g}}
\)
For the old time period \( T_{\text{old}} \) (without the electric field):
\(
T_{\text{old}} = 2\pi \sqrt{\frac{l}{g}}
\)
For the new time period \( T_{\text{new}} \) (with the electric field):
\(
T_{\text{new}} = 2\pi \sqrt{\frac{l}{g_{\text{eff}}}} = 2\pi \sqrt{\frac{l}{\frac{g}{2}}} = 2\pi \sqrt{\frac{2l}{g}}
\)
Step 5: Find the ratio of the new time period to the old time period
Now we can find the ratio of the new time period to the old time period:
\(
\frac{T_{\text{new}}}{T_{\text{old}}} = \frac{2\pi \sqrt{\frac{2l}{g}}}{2\pi \sqrt{\frac{l}{g}}} = \frac{\sqrt{2l}}{\sqrt{l}} = \sqrt{2}
\)
Step 6: Final ratio
Thus, the ratio of the new time period to the old time period is:
\(
\frac{T_{\text{new}}}{T_{\text{old}}} = \sqrt{2} : 1
\)
Conclusion
The ratio of the new time period to the old time period is \( \sqrt{2} : 1 \).
---
A particle of mass m and charge q is oscillating in simple harmonic motion (SHM) from a string of length l. When a vertical electric field of magnitude \( E = \frac{mg}{2q} \) is applied, we need to find the ratio of the new time period to the old time period of the oscillation.
The force \( F \) on the particle due to the electric field \( E \) is given by:
\(
F = qE
\)
Substituting the value of \( E \):
\(
F = q \left(\frac{mg}{2q}\right) = \frac{mg}{2}
\)
Here, the charge \( q \) cancels out.
The effective force acting on the particle is the gravitational force minus the force due to the electric field:
\(
F_{\text{effective}} = mg - \frac{mg}{2} = \frac{mg}{2}
\)
Thus, the effective acceleration \( g_{\text{eff}} \) acting on the particle is:
\(
g_{\text{eff}} = \frac{mg_{\text{effective}}}{m} = \frac{g}{2}
\)
The time period \( T \) of a simple harmonic oscillator is given by:
\(
T = 2\pi \sqrt{\frac{l}{g}}
\)
For the old time period \( T_{\text{old}} \) (without the electric field):
\(
T_{\text{old}} = 2\pi \sqrt{\frac{l}{g}}
\)
For the new time period \( T_{\text{new}} \) (with the electric field):
\(
T_{\text{new}} = 2\pi \sqrt{\frac{l}{g_{\text{eff}}}} = 2\pi \sqrt{\frac{l}{\frac{g}{2}}} = 2\pi \sqrt{\frac{2l}{g}}
\)
Now we can find the ratio of the new time period to the old time period:
\(
\frac{T_{\text{new}}}{T_{\text{old}}} = \frac{2\pi \sqrt{\frac{2l}{g}}}{2\pi \sqrt{\frac{l}{g}}} = \frac{\sqrt{2l}}{\sqrt{l}} = \sqrt{2}
\)
Thus, the ratio of the new time period to the old time period is:
\(
\frac{T_{\text{new}}}{T_{\text{old}}} = \sqrt{2} : 1
\)
The ratio of the new time period to the old time period is \( \sqrt{2} : 1 \).
Similar Questions
A particle of mass 'm' and charge 'q' is suspended from the ceiling with the help of an insulating wire of length 'l'. It is placed in an uniform electric field as shown in figure. Then the time period of oscillation is
_2019_CBT6_E01_041_Q01.png)
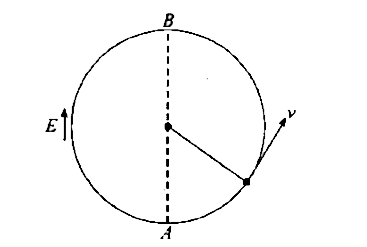
View SolutionA particle of mass m and charge Q is attached to a string of length l. It is whirled in a vertical circle in the region of an electric field E as shown in the figure-5.105.What is the speed given to the particle at the point B,so that tension in the string when the particle is at A is ten times the weight of the particle?
View SolutionA particle of mass m carrying a positive charge q moves simple harmonically along the x-axis under the action of a varying electric field E directed along the x-axis. The motion of the particle is confined between x=0 and x=2l. The angular frequency of the motion is ω. Then which of the following is correct ?
View SolutionA thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=mg2q. The rod is released from, shown position from rest.

What is the speed of ball when rod becomes vertical?
View SolutionA thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=mg2q. The rod is released from, shown position from rest.

What is the angular acceleration of the rod at the instant of releasing the rod?
View SolutionA thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=mg2q. The rod is released from, shown position from rest.

What is the acceleration of the small ball at the instant of releasing the rod?
View SolutionA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
View SolutionA ball having charge q and mass m is suspended from a string of length L between two parallel plates where a vertical electric field E is established . Find the time period of simple pendulum if electric field is directed (a) downward and (b) upward.
View SolutionA particle starts oscillating simple harmonically from its equilibrium position then, the ratio of kinetic energy and potential energy of the particle at the time T/12 is: (T=time period)
View SolutionA charged ball of mass m and charge q is projected from the ground with an initail velocity u and angle of projection θ at the time of projection vertically upward electric field E is switched on. When it reaches the maximum height electric filed is switched off and a horizontal electric feild of same magnitude E is switched on. Then answer the following question (Assume mg> qE)
Q In the above experiment
View Solution
