A ball having charge q and mass m is suspended from a string of length L between two parallel plates where a vertical electric field E is established . Find the time period of simple pendulum if electric field is directed (a) downward and (b) upward.
To solve the problem of finding the time period of a simple pendulum with a charged ball suspended in an electric field, we will analyze two cases: when the electric field is directed downward and when it is directed upward.
Given:
- Charge of the ball = q
- Mass of the ball = m
- Length of the string = L
- Electric field strength = E
(a) When the electric field is directed downward:
1. Identify the Forces:
- The gravitational force acting on the ball is Fg=mg (downward).
- The electric force acting on the ball due to the electric field is Fe=qE (also downward, since the electric field is directed downward).
2. Calculate the Net Force:
- Since both forces act in the same direction (downward), the net force Fnet is:
Fnet=Fg+Fe=mg+qE
3. Determine the Net Acceleration:
- The net acceleration a can be calculated using Newton's second law:
a=Fnetm=mg+qEm=g+qEm
4. Calculate the Time Period:
- The formula for the time period T of a simple pendulum is given by:
T=2π√La
- Substituting the expression for a:
T=2π
⎷Lg+qEm
(b) When the electric field is directed upward:
1. Identify the Forces:
- The gravitational force acting on the ball remains Fg=mg (downward).
- The electric force acting on the ball due to the electric field is Fe=qE (upward).
2. Calculate the Net Force:
- Since the forces act in opposite directions, the net force Fnet is:
Fnet=Fg−Fe=mg−qE
3. Determine the Net Acceleration:
- The net acceleration a is:
a=Fnetm=mg−qEm=g−qEm
4. Calculate the Time Period:
- Using the formula for the time period T:
T=2π√La
- Substituting the expression for a:
T=2π
⎷Lg−qEm
Summary of Results:
- Time Period when Electric Field is Downward:
T=2π
⎷Lg+qEm
- Time Period when Electric Field is Upward:
T=2π
⎷Lg−qEm
- Charge of the ball = q
- Mass of the ball = m
- Length of the string = L
- Electric field strength = E
- The gravitational force acting on the ball is Fg=mg (downward).
- The electric force acting on the ball due to the electric field is Fe=qE (also downward, since the electric field is directed downward).
- Since both forces act in the same direction (downward), the net force Fnet is:
Fnet=Fg+Fe=mg+qE
- The net acceleration a can be calculated using Newton's second law:
a=Fnetm=mg+qEm=g+qEm
- The formula for the time period T of a simple pendulum is given by:
T=2π√La
- Substituting the expression for a:
T=2π
⎷Lg+qEm
- The gravitational force acting on the ball remains Fg=mg (downward).
- The electric force acting on the ball due to the electric field is Fe=qE (upward).
- Since the forces act in opposite directions, the net force Fnet is:
Fnet=Fg−Fe=mg−qE
- The net acceleration a is:
a=Fnetm=mg−qEm=g−qEm
- Using the formula for the time period T:
T=2π√La
- Substituting the expression for a:
T=2π
⎷Lg−qEm
- Time Period when Electric Field is Downward:
T=2π
⎷Lg+qEm
- Time Period when Electric Field is Upward:
T=2π
⎷Lg−qEm
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 5
5 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Example Type 6
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A particle of mass m and charge q is oscillating simple harmonically from a string of length l.Now a vertical electric field of magnitude E=mg2q is switched on.The ration of new time period to old time period is
View SolutionA positively charged particle of charge q and mass m is suspended from a point by a string of length l. In the space a uniform horizontal electric field E exists . The particle is drawn aside so that it is projected horizontally with velocity v such that the particle starts to move along a circle with same constant speed v. Find the speed v.

View Solution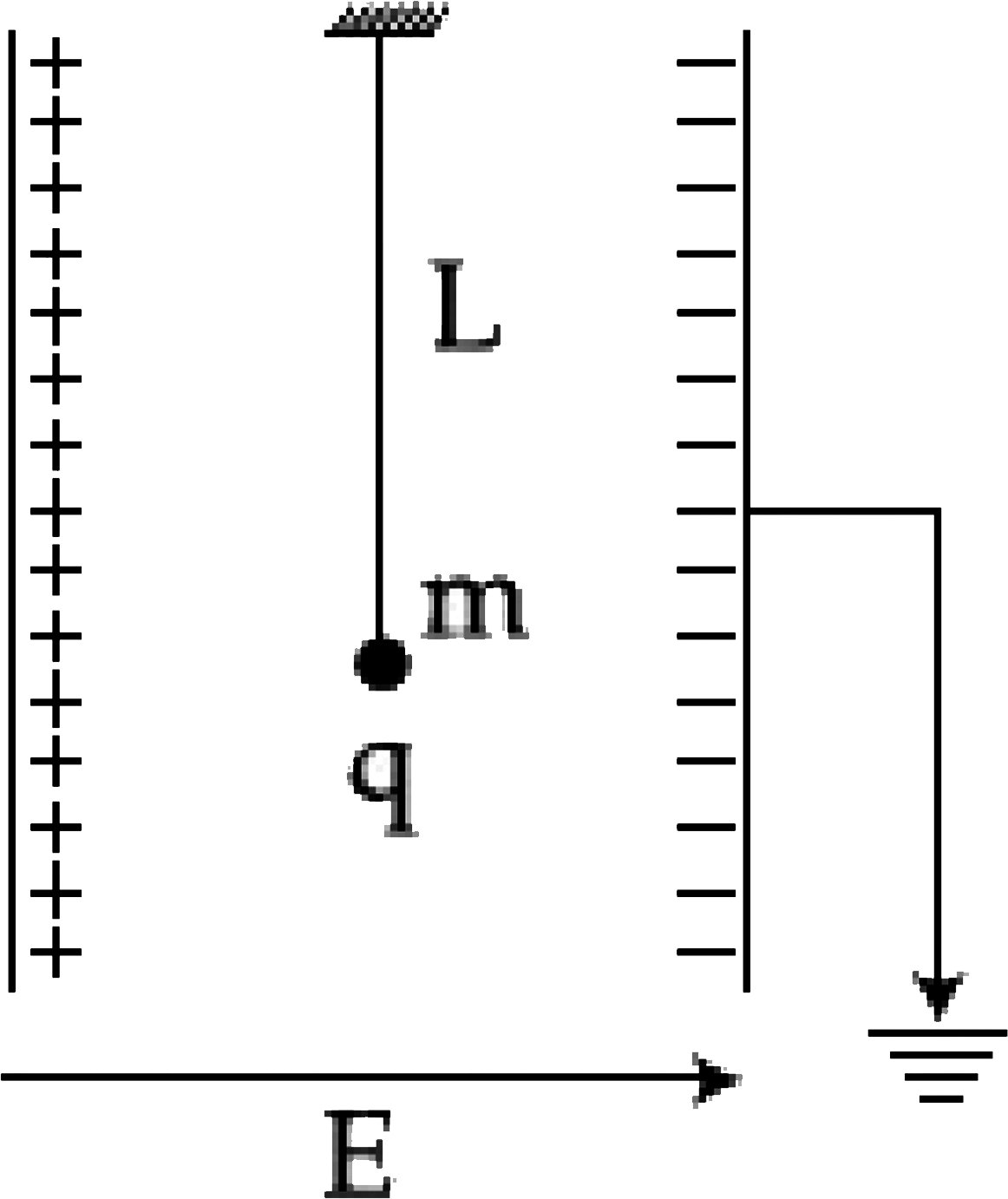
A simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:
View SolutionA simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:
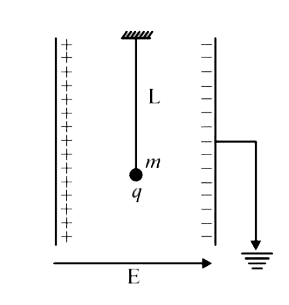
View SolutionA simple pendulum of length L is placed between the plates of a parallel plate capacitor having electric field E, as shown in figure. Its bob has mass m and charge q. The time period of the pendulum is given by:

View SolutionA particle of mass 'm' and charge 'q' is suspended from the ceiling with the help of an insulating wire of length 'l'. It is placed in an uniform electric field as shown in figure. Then the time period of oscillation is
_2019_CBT6_E01_041_Q01.png)
View SolutionA point charge q is situated at X between two parallel plates which have a potential difference V and carry charges +Q and −Q. What is the electric field strength at X ?

View SolutionAn electron having charge 'e' and mass 'm' is moving a uniform electric field E. Its acceleration will be
View SolutionA ball of mass m having a charge q is released from rest in a region where a horizontal electric field E exists.
(a) Find the resultant force acting on the ball.
(b) Find the trajectory followed by the ball.
View SolutionTwo identical balls , each having a charge q and mass m , are suspended from a common point by two insultating strings each of length L. The balls are held at a separation x and then released. Find
(a) the electric force on each ball
(b) the component of the resultant force on a ball along and perpendicular to string
(c ) the tension in the string
(d) the acceleration of one of the balls. Consider the situation only for the instant just after the release.
View Solution
