A rectangular coil of area A rotates in a uniform magnetic field B with angular velocity about an axis perpendicular to the field, initially the plane of coil is perpendicular to the field,then the avarage induced e.m.f. after rotating by is
A.
B.
C.
D.
To solve the problem of finding the average induced e.m.f. in a rectangular coil rotating in a uniform magnetic field, we can follow these steps:
1. Understand the Initial Conditions:
- The coil is rectangular with an area A.
- It rotates in a uniform magnetic field B.
- Initially, the plane of the coil is perpendicular to the magnetic field, meaning the angle θ=0∘.
2. Calculate Initial Magnetic Flux:
- The magnetic flux Φ through the coil is given by:
Φ=B⋅A⋅cos(θ)
- Initially, since θ=0∘:
Φinitial=B⋅A⋅cos(0)=B⋅A
3. Determine the Magnetic Flux After 90° Rotation:
- After the coil rotates by 90∘, the angle θ becomes 90∘:
Φfinal=B⋅A⋅cos(90)=B⋅A⋅0=0
4. Calculate the Change in Magnetic Flux:
- The change in magnetic flux ΔΦ is:
ΔΦ=Φfinal−Φinitial=0−(B⋅A)=−B⋅A
5. Determine the Time Taken for the Rotation:
- The angular velocity ω is defined as the rate of rotation in radians per second.
- The time period T for one complete rotation (360°) is given by:
T=2πω
- The time taken to rotate 90∘ (which is 14 of a full rotation) is:
Δt=T4=2π4ω=π2ω
6. Calculate the Average Induced e.m.f.:
- According to Faraday's law of electromagnetic induction, the average induced e.m.f. E is given by the change in magnetic flux divided by the time taken:
E=−ΔΦΔt
- Substituting the values we have:
E=−−B⋅Aπ2ω=2B⋅A⋅ωπ
Final Answer:
The average induced e.m.f. after rotating by 90∘ is:
E=2BAωπ
- The coil is rectangular with an area A.
- It rotates in a uniform magnetic field B.
- Initially, the plane of the coil is perpendicular to the magnetic field, meaning the angle θ=0∘.
- The magnetic flux Φ through the coil is given by:
Φ=B⋅A⋅cos(θ)
- Initially, since θ=0∘:
Φinitial=B⋅A⋅cos(0)=B⋅A
- After the coil rotates by 90∘, the angle θ becomes 90∘:
Φfinal=B⋅A⋅cos(90)=B⋅A⋅0=0
- The change in magnetic flux ΔΦ is:
ΔΦ=Φfinal−Φinitial=0−(B⋅A)=−B⋅A
- The angular velocity ω is defined as the rate of rotation in radians per second.
- The time period T for one complete rotation (360°) is given by:
T=2πω
- The time taken to rotate 90∘ (which is 14 of a full rotation) is:
Δt=T4=2π4ω=π2ω
- According to Faraday's law of electromagnetic induction, the average induced e.m.f. E is given by the change in magnetic flux divided by the time taken:
E=−ΔΦΔt
- Substituting the values we have:
E=−−B⋅Aπ2ω=2B⋅A⋅ωπ
The average induced e.m.f. after rotating by 90∘ is:
E=2BAωπ
Similar Questions
A coil is rotated in a uniform magnetic field about an axis perpendicular to the field. The emf induced in the coil would be maximum when the plane of coil is :
View SolutionA rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the

View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
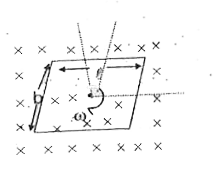
A rectangular loop of length l and breadth b is situated in a uniform magnetic field of induction B with its plane perpendicular to the field as shown in the figure . Calculate the rate of change of magnetic flux and the induced emf if the loop is rotated with constant angular velocity ω
(a) about an axis passing through the centre and perpendicular to the loop.
(b) about an axis passing through the centre parallel to the breadth through angle 180∘ .
View SolutionA rectangular copper coil is placed in a uniform magnetic field of induction 40 mT with its plane perpendicular to the field. The area of the coil is shrinking at a constant rate of 0.5m2s−1. The emf induced in the coil is
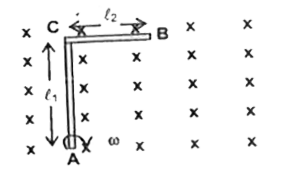
View SolutionFor an L shaped conducting rod placed in an uniform magnetic field →B rotating with constant angular velocity ω about an axis passing through one of its ends A and normal to the plane of the conductor induced emf
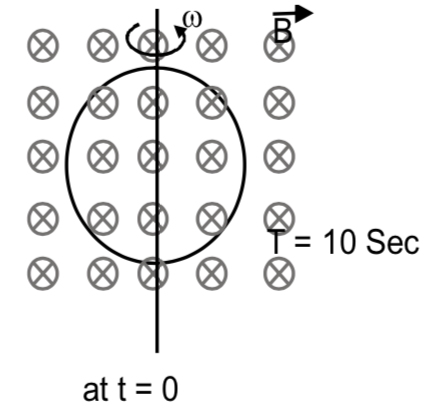
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively. (Figure:
 )
)
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field.If T=10sec, find the instant of time at which EMF will be maximum & minimum respectively :
View SolutionA ring rotates with angular velocity ω about an axis perpendicular to the plane of the ring passing through the center of the ring.A constant magnetic field B exists parallel to the axis.Find the emf induced in the ring.

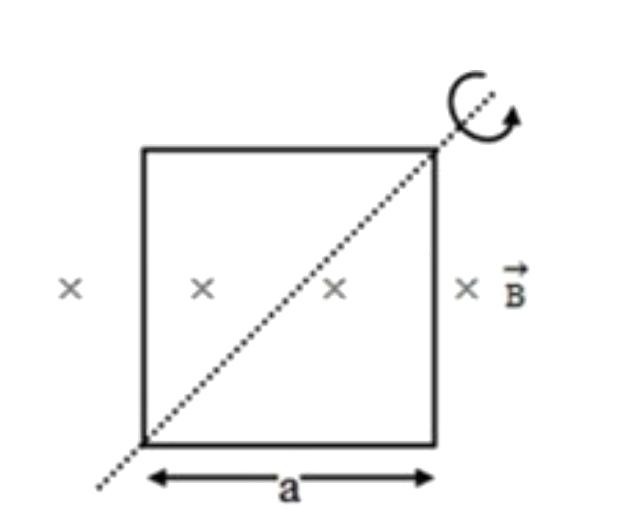
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
View Solution